Нас просят найти расстояние между АК И BC. AB=3\sqrt[2]{5}
Объяснение:Из единственности перпендикуляра между скрещивающимися прямыми из рисунка понятно что это и есть прямая АВ.
По теореме о трех перпендикулярах Треугольник КВС прямоугольный и прямым углом является угол КВС и по теореме пифагора ВС равен 81-49=32 ,извлекаем из под корня и ВС равен 4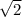 .
.
Также BC=AD
Из треугольника КАD по теореме пифагора получаем КА=2 и из треугольника КСА вычисляем диагональ прямоугольника АС=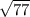
По теореме Пифагора вычитаем из квадрата АС квадрат BC
![AC^{2} -BC^{2}=AB^{2}\\AB=3\sqrt[2]{5}](/tpl/images/0138/1590/89535.png)

Один из сторон — перпендкулярен прямой, тоесть эта же сторона образует 2 прямых угла, тоесть, треугольник — прямоугольный.
Наклонная(или гипотенуза) — равна 12 сантиметров, и с прямой она образует угол 30-и градусов.
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы
А перпендикуляр лежит на против этого же угла 30-градусов, тоесть — прерпендикуляр равен половине наклонной, тоесть перпендикуляр равен: 12/2 = 6.
Теперь мы знаем гипотенузу, и один и катетов, чтобы найти проекцию(второй катет) — используем теорему Пифагора: 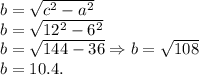
Вывод: перпендикуляр равен — 6 см; проекция равна — 10.4см(или √108, как удобнее).
Соединим центр О с точками А и В отрезками. Получим равнобедренный треуг.АОВ с основанием АВ. Т.к. К-середина АВ, то ОК-медиана, а следовательно, биссектриса и высота в треугольнике АОВ. Следовательно угол ОКА=90 градусов. Угол АОК=60/2=30 градусов. Угол ОАК равен 90-30=60 градусов.
ответ: углы треугольника АОК равны 30, 60 и 90 градусов.