Добавляешь угол 6, вертикальный с углом 5, угол 7 смежный с углом 1(он должен быть слева) и отмечаешь левую секущую буквой с, а правую буквой с с индексом 1
/_(значок угла)
1./_5=/_6=80°(по свойству вертикальных углов)
2. /_6 и /_4 - равные накрест лежащие углы, образованные секущей c при прямых a и b, а значит a || b по 1-му признаку параллельности прямых (если накрест лежащие углы равны, то прямые параллельны, возможно у вас это другой по счёту)
3./_3=/_7=180° (свойство параллельных прямых)
4./_1=180°-/_7=180°-125°=55°(свойство смежных углов)
5./_2=180°-/_3=180°-125°=55°(свойство смежных углов)
6. /_1-/_2=55°-55°=0°
Не знаю почему так получилось, вроде всё правильно делал
Билет 1.
1. Точка и прямая - основные фигуры на плоскости. Они не имеют определения. Точка не имеет размеров (длины, ширины, радиуса). Точки обозначаются заглавными латинскими буквами.
Прямая бесконечна. Ее можно представить как туго натянутую нить, бесконечную в обе стороны. На рисунке изображается часть прямой. Прямая обозначается по названию двух точек, лежащих на ней, или строчной латинской буквой.
Отрезок - это часть прямой, ограниченная точками с двух сторон. Точки, ограничивающие отрезок, называются его концами. Отрезок имеет длину. Отрезок обозначается двумя заглавными латинскими буквами - по названию его концов.
2. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство. Построим треугольник А₁В₁С₁, совместив равные стороны АС и А₁С₁ данных треугольников, как на рисунке, так, чтобы вершины В и В₁ оказались по разные стороны от прямой АС.
Тогда ΔВАВ₁ равнобедренный и значит ∠1 = ∠2 как углы при основании равнобедренного треугольника,
ΔВСВ₁ равнобедренный и ∠3 = ∠4, ⇒
∠АВС = ∠АВ₁С и значит ΔАВС = ΔА₁В₁С₁ по двум сторонам и углу между ними.
Билет 2.
1. В зависимости от вида углов треугольники бывают:
остроугольные (все углы острые);прямоугольные (один угол прямой);тупоугольные (один угол тупой);В зависимости от сторон:
разносторонние (нет равных сторон);равнобедренные (две стороны равны);равносторонние (все стороны равны).2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Дано: с∩а, c∩b, ∠1 = ∠2.
Доказать: a║b.
Доказательство:
∠3 = ∠1 как вертикальные,
∠2 = ∠1 по условию, значит
∠3 = ∠2, а эти углы - накрест лежащие при пересечении прямых а и b секущей с, значит а║b по первому признаку параллельности прямых (по накрест лежащи углам).
Сразу поправлю: часть круга, ограниченная дугой и её хордой называется сегментом.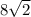 см)
см)
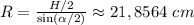
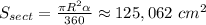
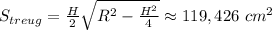
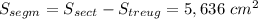
Его площадь равна площади сектора минус площадь треугольника AOB.
обозначения: точка O -центр круга; точки A, B -концы хорды
H -длина хорды (как я понял, равна
α -центральный угол AOB (для удобства в формулах)
Считать будем округлённо (если выразить ответ точно, то получится кучка дробей и радикалов).
В равнобедренном треугольнике AOB проведём высоту (пройдёт от точки O до центра хорды). Получим два прямоугольных треугольника- их гипотенуза равна радиусу круга, острый угол равен половине угла α. В прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к гипотенузе. Используя это, выразим и найдём радиус:
Найдём площадь сектора:
Найдём площадь равнобедренного треугольника AOB по формуле:
И, наконец найдём площадь сегмента: