3) Р=40 ед
4) Р=22 ед
Объяснение:
3) если опустить ⊥ ВМ из вершины В на сторону АД получим прямоугольный ΔАВМ, ВМ- противолежащий катет, АВ - гипотенуза, ∠А=30
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе
тогда 5/АВ=sin30
5/AB=1/2
AB=10
Так как в ромбе все стороны равны АВ*4=40 - это и будет искомый периметр
4) мы знаем по условию что АВ+ВС+СД+АД=32 ед
Нам нужно найти АВ+ВЕ+АЕ
так как СД=ВЕ, ВС=5 и АД=АЕ+5, то можем записать
АВ+5+ВЕ+АЕ+5=32 ед
АВ+ВЕ+АЕ=22 ед
30
Объяснение:
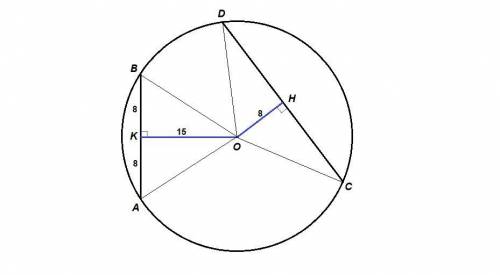
Соединим центр окружности с концами хорд.
ОА = ОВ = ОС = OD как радиусы.
Проведем ОК⊥АВ и ОН⊥CD.
ОК = 15, ОН = 8 - расстояния от центра до хорд АВ и CD соответственно.
ΔАОВ равнобедренный, значит ОК - высота и медиана.
АК = КВ = 1/2АВ = 8
Из прямоугольного треугольника АОК по теореме Пифагора:
ОА = √(AK² + OK²) = √(8² + 15²) = √(64 + 225) = √289 = 17
ОС = ОА = 17
Из прямоугольного треугольника СОН по теореме Пифагора:
СН = √(CO² - OH²) = √(17² - 8²) = √(289 - 64) = √225 = 15
ΔOCD равнобедренный, значит ОН - высота и медиана.
CD = 2CH = 2 · 15 = 30
1. 120 см²
2. 36√3 см²
3. 270 см²
Объяснение:
на фото рисунок и дано
1) ΔABC=ΔADC, по трём сторонам => Sabcd=2*SΔabc
По формуле герона
р=(10+13+13):2=36/2=18 см
S²Δabc=p(p-10)(p-13)(p-13)
S²Δabc=18*8*5*5
SΔabc=√(18*8*5*5)=√(9*2*4*2*5*5)=3*2*2*5=60 см²
Sabcd=2*SΔabc=2*60=120 см²
2) Найдем угол при основе (в равнобедренном треугольнике углы при основе равны)
<CAB=<ACB=(180°-<ABC)/2=(180°-60°)/2=120°/2=60°
Если все углы в трегуольнике равны 60°, то это равносторонний треугольник, поэтому все стороны ΔABC равны 12 см
Формула площади равностороннего треугольника: SΔabc=(AB²√3):4=(12²√3):4=(144√3):4=36√3 см²
3) Чтобы найти площадь прямоугольника, андо знать его обе стороны
Рассмотрим прямоугольный треугольник ΔABC. По теореме Пифагора найдем один из его катетов--ВС--,который является и неизвестной стороной прямоугольника
ВС²=АС²-АВ²=17²-8²=(17-8)(17+8)=9*25
ВС=√(9*25)=3*5=15 см
Sabcd=AB*ВС=8*15=270 см²