<var>S=21ahaS=21∗16∗11=88hb=b2S=222∗88=8</var>
1. Касательные проведнные с одной точки равны между собой, поэтому
AC = AB = 12 см.
По теореме Пифагора
AO=корень(CO^+AC^2)=корень(9^2+12^2)=15 см
ответ: 12 см, 15 см
2. Извини, но незнаю
3. Хорды MN и PK пересекаются в точке E так, что ME = 12 см, NE = 3 см, PE = KE. Найдите PK.
По свойству хорд
ME*NE=PE*KE
Пусть PE = KE=х см
Тогда x^2=12*3=36
x>0, поєтому х=6 см
PK=PE+KE=6см+6см=12 см
ответ:12 см
4.Треугольник ОАВ равнобедренный, ОА=ОВ=16 см (радиусы);
∠А=∠В=30° - по условию;
ОН - высота ОАВ, равна 16/2=8 см (катет против угла 30°);
АВ=2*АН=2*√(16²-8²)=16√3 см.
Треугольник СОВ равнобедренный, ОС=ОВ=16 см (радиусы);
∠С=∠В=45° ⇒ ∠О=90° - прямоугольный ⇒ СВ=√(16²+16²)=16√2 см.
АВ=16√3 см;
ВС=16√2 см.
8 см
Объяснение:
Пусть CH - высота, проведенная к стороне AB, а AT - высота, проведенная к BC.
Найдем площадь ΔABC:
S1 =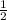 *
* 
S2 =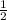 *
* 
S1 = S2 ⇒ AB * CH = BC * AT ⇒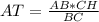
Подставив значения сторон, получим:
AT = 8 (см)