Площадь круга находят по формуле
S =πr²
Радиус вписанного в треугольник круга можно найти по формуле
r=S:p, где S- площадь треугольника, р- его полупериметр.
р=(10+24+26):2=30
Площадь треугольника найдем по формуле Герона:
S=√{(p−a)(p−b)(p−c)}, где р- полупериметр треугольника, а, b и с - его стороны.
S=√(30•20•6•4)= √(6•5•5•4•6•4)=6•5•4=120
r=120:30=4 см
S =16π см²
Радиус найти будет проще, если заметить, что отношение сторон этого треугольника из так называемых Пифагоровых троек, а именно 10:24:26=5:12:13 Это отношение сторон прямоугольного треугольника.
Тогда по формуле радиуса вписанной в прямоугольный треугольник окружности
r=(a+b-c):2, где а, b - катеты, с - гипотенуза:
r=(10+24-26):2=4 cм.
Площадь круга, естественно. будет та же - 16π см²
Площадь круга находят по формуле
S =πr²
Радиус вписанного в треугольник круга можно найти по формуле
r=S:p, где S- площадь треугольника, р- его полупериметр.
р=(10+24+26):2=30
Площадь треугольника найдем по формуле Герона:
S=√{(p−a)(p−b)(p−c)}, где р- полупериметр треугольника, а, b и с - его стороны.
S=√(30•20•6•4)= √(6•5•5•4•6•4)=6•5•4=120
r=120:30=4 см
S =16π см²
Радиус найти будет проще, если заметить, что отношение сторон этого треугольника из так называемых Пифагоровых троек, а именно 10:24:26=5:12:13 Это отношение сторон прямоугольного треугольника.
Тогда по формуле радиуса вписанной в прямоугольный треугольник окружности
r=(a+b-c):2, где а, b - катеты, с - гипотенуза:
r=(10+24-26):2=4 cм.
Площадь круга, естественно. будет та же - 16π см²
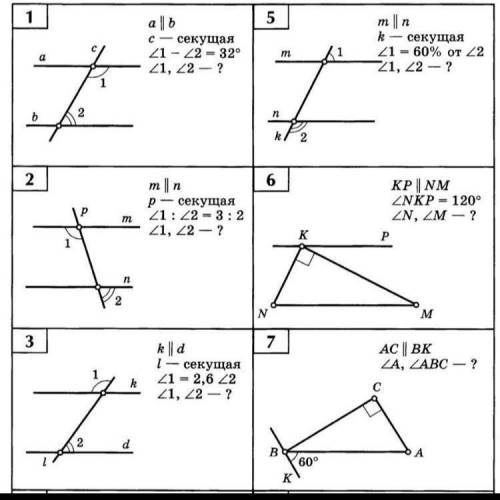
1.
Скобки=угол)
(1)-(2)=32
(1)+(2)=180
(1)=32+(2)
2*(2)=180-32
(2)=74
(1)=106
2.
(1):(2)=3:2
(1)+(2)=180
Пусть х - коэффициент пропорцианальности, тогда
3х+2х=180
5х=180
х=36
(1)=108
(2)=72
3.
(1)=2.6(2)
(1)+(2)=180
2.6(2)+(2)=180
(2)=180:3.6=50
(1)=130
5.
(1)=0.6*(2)
(1)+(2)=180
0.6(2)+(2)=180
(2)=180:1.6=112.5
(1)=67.5
Объяснение: