1)
BK биссектриса, тогда ABK=KBC или ABD+DBK=CBM+KBM откуда ABD=CBM=y и DBK=x по теореме Штейнера получается
AD*AM/(CM*CD) = (AB/BC)^2 но так как AM=CM (медиана) AD/CD = (AB/BC)^2 (1) с одной стороны AD=AB*siny и CD=BC*sin(2x+y) из прямоугольных треугольников ABD и CBD соответственно.
с другой AB/BC = cos(2x+y)/cosy из треугольника ABC Подставляя в (1) откуда siny/sin(2x+y) = cos(2x+y)/cosy откуда sin2x*cos(2x+2y)=0, x<180
откуда x=45-y
Значит ABC=2x+2y = 2*(x+45-x) = 90 гр
второй
Опишем около треугольника ABC окружность, пусть X,H,Y точки пересечения BM,BK,BD с описанной окружностью.
Тогда из условия следует AX=CY и AH=CH (опираются на равные углы) так же получаем что H середина дуги XY так как BK биссектриса, HM высота и биссектриса равнобедренного треугольника AHC и XY || AC (так как AXYC) равнобедренная трапеция , значит BYX=BDA=90 гр, если F точка пересечения XY и MH тогда из подобия треугольников XHM и XYB учитывая что XH=HY откуда XM/BX=1/2 то есть BM=MX а так как MX=MY (треугольники AMX и CMY равны) получаем BM=MX=MY треугольник BMY равнобедренный , откуда BD=YD откуда M центра описанной окружности, значит AC диаметр откуда ABC=90 гр.
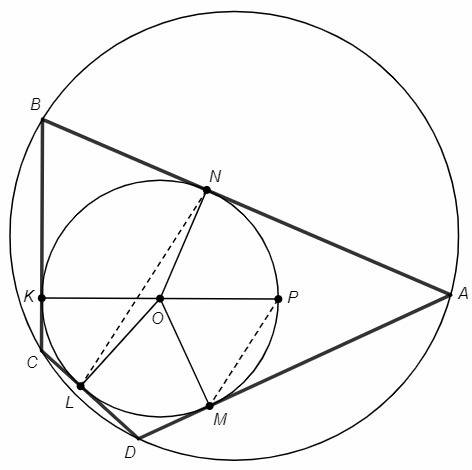
1) Окружность с центром О, диаметр KP.
2) Точки L, M на полуокружности.
3) Прямая LN||MP (точка N на окружности).
4) Касательные через точки K, L, M, N.
Пересечение касательных, проведенных через соседние точки - вершины вписанно-описанного четырехугольника.
Четырехугольник ABCD описанный по построению (стороны являются касательными к окружности).
∠KOL+∠LOP=180 (смежные углы)
∪LM=∪NP (дуги между параллельными LN и MP)
∠LOM=∠NOP => ∠LOP=∠MON => ∠KOL+∠MON=180
В четырехугольниках AMON, CKOL противолежащие прямые углы (касательная перпендикулярна радиусу), следовательно сумма другой пары углов также равна 180.
∠A+∠MON=180, ∠C+∠KOL=180 => ∠A+∠C=180
В четырехугольнике ABCD сумма противолежащих углов равна 180, следовательно он вписанный.
Четырёхугольник является описанным только тогда, когда суммы его противолежащих сторон равны.
Выпуклый четырёхугольник является вписанным только тогда, когда сумма его противолежащих углов равна 180.
Свойства вписанно-описанного четырёхугольника:
a, b, c, d - стороны
S=√(abcd)
R - радиус описанной окружности, r - радиус вписанной окружности, k - расстояние между центрами окружностей.
1/(R+k)^2 +1/(R-k)^2 =1/r^2
тк AC биссектриса углы BAC =САВ значит ВАС=45 а угол В=180-95-45=40
угол А=45+45=90 а угол D=180-А-В, D=180-90-40
Объяснение: