
Основания равнобокой трапеции равны 8 см и 18 см. Точка удалена от каждой стороны трапеции на 10 см. Найдите расстояние от этой точки до плоскости трапеции.
———————
ответ: 8 см.
Объяснение:
Назовем данную точку Е.
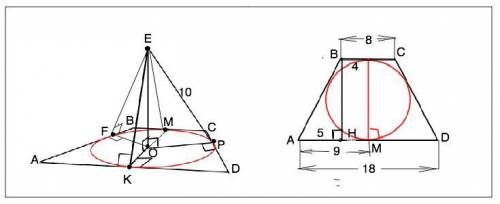
Точка удалена от каждой стороны трапеции на равное расстояние, т.е. на длину перпендикуляров, проведенных от этой точки к сторонам трапеции (см. рисунок во вложении.)
ЕК=ЕF=EM=EP.
Искомое расстояние - перпендикуляр ЕО к плоскости трапеции. Прямоугольные треугольники ЕOF=EOM=EОP=EOK, проекции их гипотенуз - по т. о 3-х перпендикулярах - перпендикулярны сторонам трапеции и равны радиусу вписанной в трапецию окружности.
Суммы противоположных сторон четырехугольника, в который вписана окружность, равны. ⇒ АВ+СD=BC+AD=8+18=26. Боковые стороны равны между собой (дано), ⇒ их длина 26:2=13 см.
Из вершины В трапеции опустим перпендикуляр ВН на АD. Он является высотой трапеции и равен диаметру вписанной окружности.
АН - полуразность оснований. АН=(АD-ВС):2=5.
Из ∆ АВН по т.Пифагора ВН=√(AB²-AH²)=√(13²-5²)=12 см ⇒ d= МК=12, ОК=r=12:2=6 см.
Из ∆ ЕОК по т.Пифагора ЕО=√(EK²-КО²)=√(10²-6²)=8 (см).
Следовательно, центр шара , описанного вокруг пирамиды SABC лежит в этой же точке и радиус его равен половине ребра SB. Ребро SB найдем по Пифагору: SB=√(L²+b²).
Значит OA=OC=OB=OS=Rш=(1/2)√(L²+b²), а его объем равен Vш=(4/3)*πR³ или
Vш=(4/3)*(1/8)π(L²+b²)√(L²+b²)=(1/6)*(L²+b²)√(L²+b²). (ответ).
Найдем объем пирамиды.
Опустим перпендикуляр SH из точки S на плоскость АВС. Основание этого перпендикуляра Н попадет на прямую НВ в плоскости АВС вне треугольника АВС. (То есть грань ASC не перпендикулярна плоскости основания). Чтобы найти точку Н, надо в плоскости АВС провести перпендикуляры к сторонам АВ и СВ в точки А и С. Их пересечение и даст нам искомую точку Н, в которую проецируется вершина S пирамиды, так как по теореме, обратной теореме о трех перпендикулярах, "прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции". Значит SH - искомая высота. В равнобедренном треугольнике АВС отрезок ВР - высота, биссектриса и медиана этого треугольника.
Тогда в прямоугольном треугольнике ВАН угол <ABH=(β/2), а гипотенуза НВ=b/Cos(β/2). В прямоугольном треугольнике SHB по Пифагору катет SH=√ (SB²-HB²) или
SH=√[(√(L²+b²))²-(b/Cos(β/2))²]=√[(L²+b²)-(b²/Cos²(β/2)]
Объем пирамиды Vп=(1/3)*So*H. Или
Vп=(1/3)*b²Sinβ/2*√[(L²+b²)-(b²/Cos²(β/2)]. Или
Vп=(1/6)*b²Sinβ*√[(L²+b²)-(b²/Cos²(β/2)]. (ответ).
Проверим решение на конкретных числах.
Пусть b=4, L=3, β=60.
Тогда SB=√(L²+b²)=5.
PB=√(16+4)=√12=2√3.
AH=4√3/3, SH=√(9-48/9)=√33/3. (первый вариант).
HP=2√3/3, SP=√(L²-CP²)=√5.
SH=√(SP²-HP²)=√(5-12/9)= √33/3 (второй вариант).
HB=HP+PB=8√3/3.
SH=√(SB²-HB²)=√(25-199/9)=√33/3. (третий вариант).
Из моего решения:
SH=√[(L²+b²)-(b²/Cos²(β/2)]=√[(9+16)-(16*4/3]=√(11/3)=√33/3.