В равнобедренном треугольнике высоты, проведенные к основанию и боковой стороне. равны соответственно 10 и 12 см. Найти длину основания.
ответ: 15 см.
Объяснение:
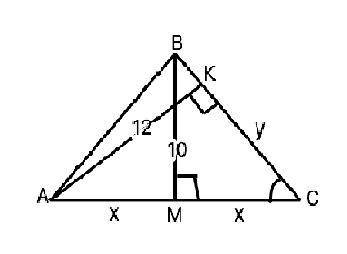
Пусть данный треугольник АВС (АВ=ВС), высоты ВМ и АК равны 10 и 12 см соответственно.
Прямоугольные треугольники АКС и МВС подобны по общему острому углу С.
Из подобия ВМ:АК=МС:КС
Примем КС=у, МС=х.
Тогда х:у=10:12, откуда у=1,2 х.
ВМ - не только высота. но и медиана р/бедренного ∆ АВС.
АС=АМ+СМ=2х
Из ⊿ АКС по т.Пифагора АС²=КС²+АК²
4х²=144+1,44х²
Для удобства сократим обе стороны уравнения на 4.
х²=36+0,36х² ⇒
х²=56,25 ⇒х=7,5
АС=2х=15 см.
ну смотри, угол между прямой и плоскостью, это угол между её проекцией и этой прямой, у тебя же дан косинус угла, если его сократить получится 24/25, у тебя дан прилежащий катет, ты можешь найти гипотенузу:
24/25 = 48/x где - х это гипотенуза
x = 50
так как у тебя даже сказано "перпендикуляр" значит треугольник прямоугольный, ну по теореме пифагора найди, то есть гипотенуза в квадрате минус катет (который равен 48 по условию) в квадрате и всё это под корнем будет равно 14 ( ну это 50 в квадрате - 48 в квадрате и всё это под корнем)
вторая аналогично.
извиняюсь за текст, пишу с компа, телефон без зарядки)
ответ: 30’