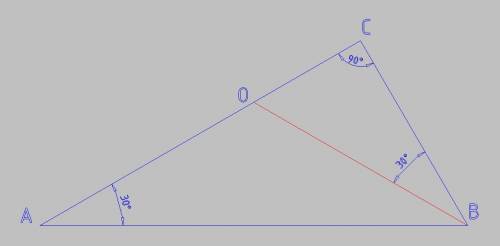
Пусть х - длина другого катета, тогда использя свойство катета , лежащего против угла в 30 град и теоремы Пифагора, сот уравнение:
144+х2=4х2, где х2 - это х в квадрате
3х2=144
х2=48
х=4корня из 3 - другой катет.
Теперь рассмотрим маленький треугольник с тем же прямым углом и биссектрисой, которая является гипотенузой, используя тоже свойство катета и опять т Пифагора сост уравнение, в котором х - длина биссектрисы:
(х2)/4+48=х2 домножаю на 4
х2+192=4х2
3х2=192 делим на 3
х2=64
х=8 это и естьдлина биссектрисы.
Объяснение:
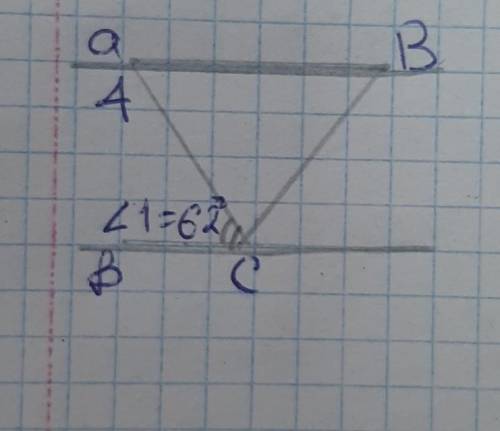
∠A= ∠1(т.к. они односторонние при секущей АС) (снаружи треугольника)
∠B=∠1(т.к. они накрест лежащие пр секущей СВ) (снаружи треугольника)
∠C= 180°-(62°+62°)= 56° (угол С внутри треугольника)
∠САВ= 180°-62°=118°
∠АВС= 180°-(62°+56°)=62°