
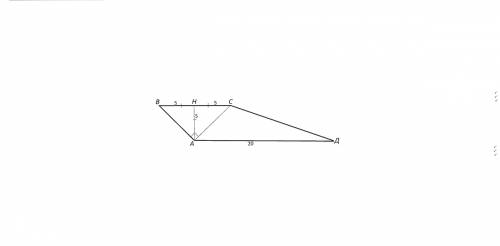
Через диагональ основания АС правильной четырехугольной призмы (основание - квадрат) параллельно диагонали B1D призмы проведено сечение АРС. Сечение - равнобедренный треугольник с высотой ОР, параллельной диагонали B1D. АС = 2√2, Sapc=2√3 (дано).
Sapc=(1/2)*AC*PO => PO=2*S/AC = √6. Треугольники BB1D и BPO подобны, так как РО параллельна B1D, а BD=2*ВО (точка О пересечения диагоналей квадрата делит их пополам). Значит коэффициент подобия итреугольников равен 2 и диагональ призмы B1D равна РО*2 = 2√6.
ответ: диагональ призмы равна 2√6.
∠ 1 и ∠ 2 соответстеные углы образованы при пересечение а и в секущей АВ.
т к ∠ 1 = ∠ 2 следовательно по свойству параллельных прямых a||в
∠3 и ∠4 односторонние образованы при пересечение а и в секущей ВС.
т к а||в по свойству параллельных прямых в сумме ∠3+∠4 дают 180° следовательно
∠4=180°-∠3=180°-140°= 40°