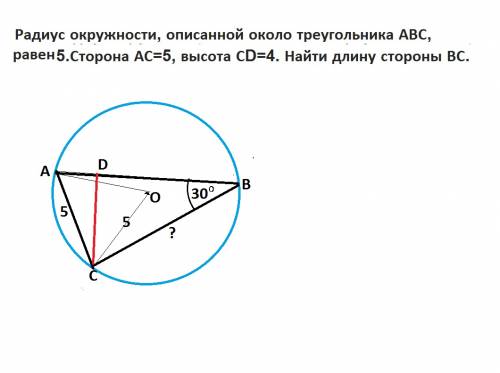
По условию сторона АС вписанного треугольника АВС равна радиусу описанной вокруг него окружности.
Следовательно, эта сторона с радиусами окружности образует равносторонний треугольник и как хорда стягивает дугу 60°.
Где бы ни находилась на окружности вершина вписанного угла, опирающегося на хорду АС, этот угол будет равен половине центрального угла, опирающегося на ту же дугу, которую стягивает эта хорда.
Угол АВС равен половине центрального угла, т.е. 30°.
Высота СД противолежит этому углу, и потому гипотенуза СВ треугольника СВD вдвое больше СD
ВС=2*СD=2*4=8
или, иначе, СВ=СD:sin(60°) =4:0,5=8

1) a(a-8)=48;
a^2 -8a - 48 = 0;
Решаем квадратное уравнение и получается 2 корня: a = -4 , a = 12;
Но длина стороны не может быть отрицательной, следовательно - одна сторона равна 12 см, а другая (12-8) = 4 см.
Периметр равен (12+4+12+4) см = 32 см.
2) a(a-3)=40;
a^2 - 3a - 40 = 0;
Решаем квадратное уравнение и получается 2 корня: a = -5 , a = 8;
Но длина стороны не может быть отрицательной, следовательно - одна сторона равна 8 см, а другая (8-3) = 5 см.
Периметр равен (8+5+8+5) см = 26 см.