Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб АВСD с острым углом α. Прямая BC1 составляет с плоскостью DC1D1 угол β. Найдите площадь боковой поверхности и объем параллелепипеда, если длина бокового ребра а.
Прямокутник АВСД, діагоналі АС та ВД перетинаються в т. О. ОН - відстань від т. О до більшої сторони прямокутника ВС (отже ОН - висота трикутника ВСО) ОМ - відстань від т. О до більшої сторони прямокутника АД (отже ОМ - висота трикутника АДО) ОР - відстань від т. О до меншої сторони прямокутника АВ (отже ОР - висота трикутника АВО) ОК - відстань від т. О до меншої сторони прямокутника СД (отже ОК - висота трикутника СДО) Оскільки Діагоналі прямокутника мають однакову довжину, а також в точці перетину діляться навпіл, значить трикутник ВСО=трикутнику АДО та трикутник АВО=трикутнику СДО. А це означає, що і висоти у попарно рівних трикутниках між собою рівні, а саме ОК=ОР, а ОН=ОМ. Нехай ОН=ОМ=Х см, тоді ОК=ОР=Х+5 см (по умові задачі сказано, що точка перетину діагоналей прямокутника лежить на відстані від більшої сторони на 5 см ближче, ніж від меншої).
У прямокутника протилежні сторони рівні. АВ=СД=ОН+ОМ=Х+Х=2Х см ВС=АД=ОР+ОК=(Х+5) +(Х+5)=2Х+10 см Периметр = сумі довжин усіх сторін прямокутника Периметр = АВ+ВС+СД+АД=44 см Отже 2Х+(2Х+10) + 2Х+(2Х+10)=44 8Х+20=44 8Х=24 Х=3 см Виходить, що АВ=СД=2Х=2*3=6 см ВС=АД=2Х+10 =2*3+10=6+10=16 см
Відповідь: сторони прямокутника АВ=СД=6 см та ВС=АД=16 см
Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб АВСD с острым углом α. Прямая BC1 составляет с плоскостью DC1D1 угол β. Найдите площадь боковой поверхности и объем параллелепипеда, если длина бокового ребра а.
Объяснение:
S(бок)=Р*L, V=S(осн.)*L ,где L-боковое ребро , перпендикулярное плоскости основания.
Пусть сторона ромба х , ∠DCB=α , ВН⊥DC. Тогда углом между плоскостью (DC₁D₁) и прямой ВС₁ будет ∠ВНС₁=β .
ΔВНС-прямоугольный , ВН=х*sinα.
ΔBHC₁-прямоугольный , ВН=ВС₁*sinβ .
ΔBCC₁ прямоугольный ,BC₁=√(x²+a²), поэтому
ВН=√(x²+a²)*sinβ . Приравняем правые части для ВН и найдем сторону ромба.
х*sinα=√(x²+a²)*sinβ , х²*sin²α=(x²+a²)*sin²β , х²*sin²α-x²*sin²β=a²*sin²β , х²*(sin²α-sin²β)=a²*sin²β , х=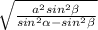 , x=
, x=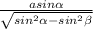 .
.
S(бок)=4а*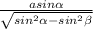 , S(бок)=
, S(бок)=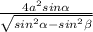 .
.
V=а²sinα*а=а³sinα
==============
Угол между прямой и плоскостью .это угол между основанием перпендикуляра и основанием наклонной.