1) определение перпендикуляра и наклонной.
пусть дана плоскость и не лежащая на ней точка.
тогда:
· отрезок прямой, перпендикулярной плоскости, соединяющий данную точку с точкой на плоскости называется перпендикуляром из данной точки к данной плоскости.
· конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
· любой отрезок, соединяющий данную точку с точкой на плоскости и не являющийся перпендикуляром к плоскости, называется наклонной.
· конец отрезка, лежащий в плоскости, называется основанием наклонной.
рис. 1.
на рисунке из точки а проведены к плоскости α перпендикуляр ав и наклонная ас. точка в - основание перпендикуляра, точка с - основание наклонной, вс - проекция наклонной ас на плоскость α.
2) доказательство того, что перпендикуляр корочек наклонной
на рисунке 2 изображена плоскость α, перпендикуляр к ней ao, наклонная ab, а также показан отрезок bo, соединяющий основания наклонной и перпендикуляра. отрезки ao, bo и ab образуют δaob.
рис. 2.
рассмотрим δaob, из определения перпендикуляра следует, что он прямоугольный. перпендикуляр ao является катетом этого треугольника, а наклонная ab – его гипотенузой. катет прямоугольного треугольника всегда меньше его гипотенузы (по теореме пифагора), следовательно, перпендикуляр всегда короче наклонной.
3) определение проекции
отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
отрезок bo на рисунке 2 – является проекцией наклонной ab.
4) теорема о сравнительной длине наклонных и их проекций
а) любая наклонная больше своей проекции.
доказательство:
вновь рассмотрим δaob, изображенный на рис. 2, из определения перпендикуляра следует, что он прямоугольный. проекция bo является катетом этого треугольника, а наклонная ab – его гипотенузой, т. к. катет прямоугольного треугольника всегда меньше его гипотенузы, следовательно, проекция наклонной на плоскость всегда короче самой наклонной.
б) равные наклонные имеют равные проекции
доказательство: рассмотрим треугольники aob и aod, они равны, т. к. равны их гипотенузы ab и ad, и углы aob и aod (они прямые), а сторона ao у них общая. из равенства треугольников следует и равенство их сторон bo = od, что и требовалось доказать.
в) если проекции наклонных равны, то и наклонные равны. доказывается аналогично утверждению б.
г) большей наклонной соответствует большая проекция.
доказательство:
рассмотрим прямоугольные треугольники aob и aod, ab > ad.
=
=
но так как ab > ad => ab2 > ad2 => > =>
=> bo > do. что и требовалось доказать.
д) из двух наклонных больше та, у которой проекция больше. доказывается аналогично г.
коала сд0хни
Объяснение:
Мәтін бойынша КЛАССТЕР жаса.
«Жазғы Олимпиада ойындары»тақырыбында берілген мәтіннен мәліметтер жинақтап, постер не сызба-кесте жасаңыз.
Бастауын ежелгі Грекия жерінен алатын әйгілі олимпиада ойындарының 2012 жылы Лондон қаласында өтетіні осыдан 7 жыл бұрын анықталып қойған еді. Еншісіне Жазғы олимпиада ойындарын өткізу бұйырған Лондон қаласы әлемдік 9 қаланың ішінен таңдап алынды.
Олимпиада ойындары 27 шілде мен 12 тамыз аралығында Ұлыбританияның астанасы Лондон қаласында өтті. Лондон Олимпиада ойындарын үш рет қабылдаған алғашқы қала болды. Оған дейін Лондон 1908 жылы және 1948 жылы қабылдаған болатын. Лондон қаласында Олимпиада алауы жағылды. Жазғы олимпиадалық ойындарының салтанатты ашылуы Елизавета II патшайымна бұйырды.
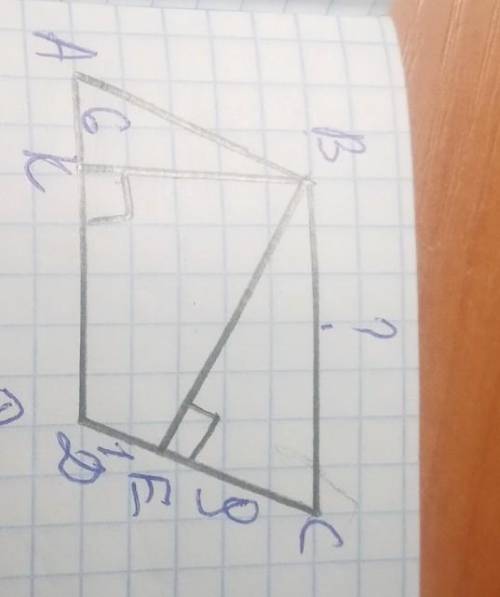
ответ: ВС= 15
Так как у параллелограмма противоположные стороны равны: АД=ВС, и найдём СД=АВ=9+1=10.
Δ АКВ ~ ΔВЕС по двум углам ( 1 признак подобия треугольников) ,так как ∠С=∠А - как противоположные углы параллелограмма равны, и ∠К=∠Е=90°
Соответственно гипотенузы этих треугольников подобны как их меньшие катеты:
АВ:ВС=АК:СЕ;
10:ВС=6:9;
ВС=9*10/6=3*5=15