* * * * * * * * * * * * * * * * * * * * * * * * * *
В равнобедренной трапеции диагональ является биссектрисой. Найдите площадь трапеции, если боковая сторона - 25 см, основание 39 см
ответ: 768 см².
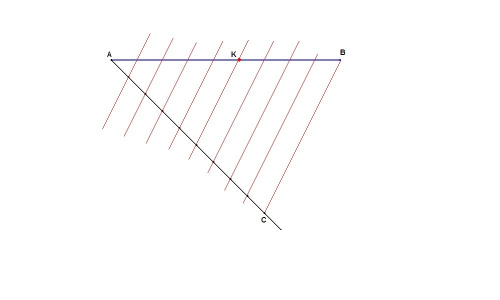
Объяснение: Пусть ABCD равнобедренная трапеция
AD и BC основания трапеции ( AD || BC ) AD =39 см ,
ВA = CD =25 см и ∠ BAC = ∠ DAC .
S(ABCD) = h*(AD+BC)/2 -?
--------------------------------------
∠ BCA= ∠ DAC как накрест лежащие углы ( BC || AD , CA секущая) ,
следовательно ∠ BCA= ∠ DAC =∠ BAC , т.е. ΔBAC равнобедренный
BA = BC =25 см получили BA = CD =25 см .
Проведем BB₁ ⊥ AD и CC₁ ⊥ AD . BCC₁B₁ _прямоугольник BB₁ =CC₁
B₁C₁ = BC =25 см ; Δ BB₁A = Δ CC₁D(гипотен. BA= CD и катеты BB₁ =CC₁).
AB₁ =(AD - BC)/2 =(39 - 25)/2 см=7 см .
Из Δ BB₁A по теореме Пифагора:
BB₁ =√(BA² -AB₁² ) =√(25² -7)² =√(625 -49) =√576=24 (см) .
* * * h=√(25²-7)² =√(25 -7)(25 +7) =√(18*32) √(9*2*16*2)=3*2*4=24 * * *
S(ABCD) = h*(AD+BC)/2 =24(39+25)/2 =24*32 = 768 (см²).

Эта задача легко решается стандартными методами. Вот нестандартное решение, позволяющее получить решение практически сразу - устно.
Если провести высоту из общей вершины наклонной боковой стороны и малого основания на большое, то трапеция будет разбита на прямоугольник и прямоугольный треугольник с одним из катетов 9 и отношением другого катета к гипотенузе 4/5. То есть это треугольник (9,12,15) (подобный египетскому).
Теперь рассмотрим треугольник, образованный диагональю, соединяющей вершину острого угла трапеции с противоположной вершиной малого основания. Это треугольник с гипотенузой 20 и катетом 12, то есть опять подобный египетскому треугольник (12,16,20) (то есть треугольник со сторонами 3,4,5, но все размеры увеличены в 4 раза).
Таким образом мы нашли и высоту трапеции 12, и боковую сторону 15, и большое основание 16, и малое, которое равно 16 - 9 = 7.
Средняя линяя равна (16+7)/2 = 11,5