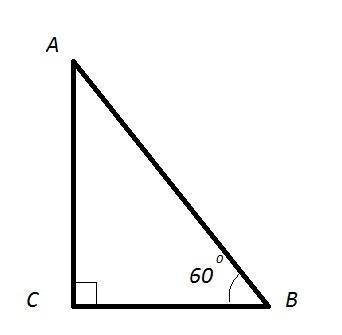
ΔАСВ - прямоугольный : АВ - гипотенуза ; АС,СВ - катеты
∠С= 90°
∠В = 60°
Сумма острых углов прямоугольного треугольника равна 90°.
Следовательно: ∠А = 90 - 60 = 30°
Катет лежащий против угла в 30° равен половине гипотенузы.
СВ = АВ/2
По теореме Пифагора:
АВ² = АС² + СВ² ⇒ АВ² = АС² + (АВ/2)²
АС= √ (АВ² - (АВ²/4)) ⇒ АС = √ ((4АВ² - АВ²)/4) = √(3АВ²/4) = (АВ*√3) /2
S =1/2 * АС * СВ = 18√3 / 3
1/2 * ((АВ*√3)/2 * (АВ/2)) = 18√3 / 3
1/2 * ( (АВ²*√3) / 4 ) = 18√3 / 3
АВ²√3 / 8 = 18√3 / 3
3 *√3* АВ² = 18√3 * 8
АВ² = 144√3 / 3√3
АВ² = 48
АВ = √48 = √(16*3) = 4√3 - гипотенуза
СВ = 4√3 /2 = 2√3 - один катет
АС = (4√3 *√ 3)/2 = (4*(√3)²)/2 = 12/2 = 6 - второй катет, который лежит против угла В = 60°.
ответ: АС = 6.
Значок вектора писаться не хочет. Поймёшь?
1. Из точки(например, В) задай вектора ВА=a, ВС= b, ВВ1=c.
2. Вырази вектора ВМ и В1С через вектора a, b, c. Для проверки: ВМ=a + 1/2b + 1\2c, В1С=b - c
3.Найди косинус угла через скалярное произведение векторов:
вектора ВМ*В1С= длина ВМ*длина В1С * cos угла.
* это пусть будет знак умножения.
ВМ*В1С= (a + 1/2b + 1\2c)*(b - c)= ab+ 1/2b( "в" квадрате) + 1/2bc - ac - 1/2bc - 1/2c( "с" в квадрате). Т.к. вектора "а", "b" и "с" ортогональны, то их произведение равны нулю.
Остаётся: = 1/2b( "в" квадрате) - 1/2c( "с" в квадрате) = 1/2*1 - 1/2*1 = 0
"в" квадрате = 1, "с" в квадрате =1
4. Если скалярное произведение ВМ*В1С = 0, это значит, что и cos угла = 0.
Отсюда следует, угол будет 90 градусов.
Длины вектора "ВМ" и "В1С" даже нет нужды вычислять.
Відповідь:
(4, 0), (-16, 0)
Пояснення:
Координата у при перетині з віссю ОХ дорівнює 0
Тому, що б знайти х, підставляємо у=0
(х+6)^2+0=100
х+6=10. або х+6= -10
х=4 або х= -16
Маємо дві точки перетину кола з Ох
(4, 0), (-16, 0)