Сумма односторонних углов равна 180°
1. 180°-118°=62°
2.180°-64=116°
3. Сумма внешнего угла с углом, по отношению к которому он является внешним, равна 180°. 180°-62°=118°. У параллелограмма 2 острых и 2 тупых угла, так 118° - больший угол, что нам и нужно.
4. 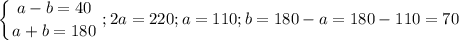
Это угол 70°
5. Наверное, сумма всех тупых углов параллелограмма.
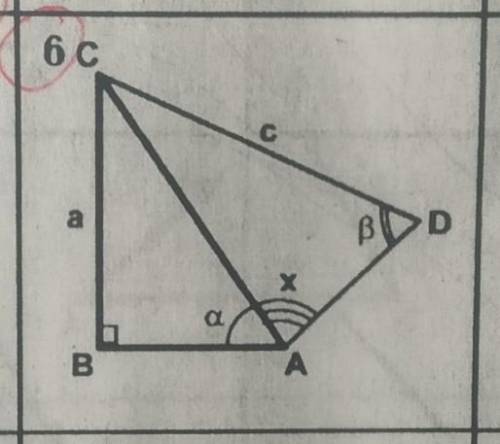
Они равны, каждый равен 260°/2=130°, острые углы равны 180°-130°=50°
6. 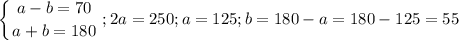
Это 55°
7. 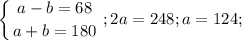
Это 124°
8. 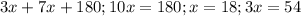
Это 54°
9. Диагональ делит параллелограмм на 2 равных треугольника. При этом 2 угла в нем известны, а третий как раз угол параллелограмма (тупой). 180°-(26°+34°)=180°-60°=120°.
Меньший угол 180°-120°=60°
10. Высота отсечет прямоугольный треугольник с одним известным острым углом 28°, второй равен 90°-28°=62°, это острый угол параллелограмма. Тупой равен 180°-62°=118°
Соразмерно условию сделаем и рассмотрим рисунок.
Противоположные стороны параллелограмма параллельны и равны.
Высота параллелограмма перпендикулярна его противоположным сторонам.
ВН ⊥ ВС и ⊥ АД
ВМ ⊥ АВ и ⊥ прямой, содержащей СД ⇒
Угол АВМ - прямой, угол АВН=90º-60º, ⇒
угол ВАН=30º
Противоположные углы параллелограмма равны. ⇒
угол ВСД= углу ВАД=30º
Катет ВН в треугольнике АВН противолежит углу 30º.
Гипотенуза в два раза больше катета, противолежащего углу 30º.
АВ=ВН:sin (30º)=6: 0,5=12 см
Катет ВМ в треугольнике ВСМ противолежит углу 30º.
ВС=ВМ:sin (30º)=16: 0,5=32 см
Площадь параллелограмма равна произведению его высоты на сторону, к которой она проведена.
S АВСД=6*32=192 см²илиS АВСД=16*12=192 см²
или
S АВСД=16*12=192 см²