Площадь трапеции S=156 см²
Объяснение:
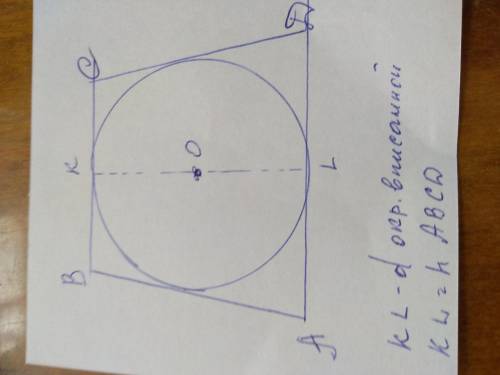
Окружность можно вписать в трапецию тогда и только тогда, когда сумма ее боковых сторон, равна сумме оснований т,е AB+CD= AD+BC
13+13=26см ( AD+BC ), отсюда - сумма оснований AB+CD=26см,
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
S=(а+b):2*h
Высота равнобокой трапеции АВСD равна диаметру вписаной окружности. Зная длинну вписанной окружности в трапецию АВСD, найдем ее диаметр по формуле: P=πd , где P-длинна окружности, которая по условию задачи равна 12πсм.
Подставляем известные значения в формулу и находим диаметр:
12π= πd
d =12π:π; d=12см
Площадь трапеции S=26:2*12=156 см²
Сторона більшого квадрата - 15 см
Площа більшого квадрата - 225 см²
Периметр більшого квадрата більше за периметр меншого в 5 разів.
Объяснение:
Сторона меншого квадрата - х см. Сторона більшого квадрата - 5х. Площа меншого квадрата - х² = 9 см². Площа більшого квадрата - (5х)². Периметр меншого квадрата - 4х. Периметр більшого квадарата - 4(5х).
З цього бачимо, що сторона (х) меншого квадрата дорівнює √9, тобто 3 см.
Тоді сторона більшого квадрата дорівнює 3 · 5 = 15 (см).
З цього площа більшого квадрата - 15² = 225 (см²)
Периметр меншого квадрата: 3 · 4 = 12 (см)
Периметр більшого квадрата: 15 · 4 = 60 (см).
Периметр більшого квадрата більше за периметр меншого в: 60 : 12 = 5 (разів)
Именно поэтому центр описанной окружности и центр вписанной окружности для этого треугольника совпадают, так как для первого - это пересечение биссектрис треугольника, а для второго - пересечение серединных перпендикуляров.
Рассмотрим треугольник АОН. Это прямоугольный треугольник с <АOH=90° и <OAH=30° (АО - биссектриса <ВАС).
Тогда АО=2*ОН, так как катет ОН лежит против угла 30°.
Но ОН - это радиус вписанной окружности, а АО - радиус описанной окружности. Значит R=2r. R=8см (дано). r=4см.
АН - это половина стороны треугольника и по Пифагору равна
АН=√(R²-r²) = √(8²-4²) = 4√3см.
Тогда сторона треугольника равна 8√3см, а его периметр равен
Р=3*8√3 =24√3см.
ответ: r=4см, Р=24√3см.