15
Объяснение:
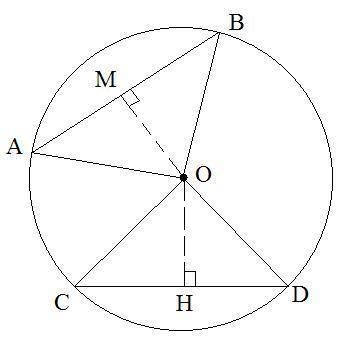
Треугольник AOB равнобедренный, так как AO=OB – как радиусы окружности. OM – расстояние от точки O до хорды AB, то есть,ОМ перпендикулярна АВ , получаем, что OM – высота и медиана (AM=MB) треугольника AOB. Так как AB=30, то AM=15. Найдем длину AO из прямоугольного треугольника AMO по теореме Пифагора:
АО= √ОМ^2+AM^2 = √8^2+15^2 = 17
Также это означает, что OC=OD=AO=17. Рассмотрим прямоугольный треугольник OCH (OH – расстояние от точки O до хорды CD) со стороной CH=CD:2=8. По теореме Пифагора находим длину OH:
OH = √OC^2-CH^2 = √17^2-8^2 = 15
Пусть угол К=х, тогда его половина - х/2
Сумма углов треуг КЛМ Л+2х=180 откуда х=90-Л/2
Сумма углов треугольника КЛN х/2+81+Л=180 откуда Л=180-81-х/2=99-(90-Л/2)/2=99-45-Л/4=44-Л/4
5/4Л=44 откуда Л=44*4/5=176/5=55,2
Угол при вершине - 55,2 град