1. Объясните, какая поверхность называется сферой и какое тело называется шаром. Выведите уравнение сферы.

2. Радиус шара равен 8 см. Через конец радиуса, лежащего на сфере, проведена плоскость под углом 45° к радиусу. Найдите площадь сечения шара этой плоскостью.

3. Концы отрезка АВ = 10 см лежат на
окружностях оснований цилиндра. Радиус Цилиндра равен 5 см, его высота 8 см.
Найдите расстояние между прямой AB иосью цилиндра.

👇

Увидеть ответ

Ответ:

makhero111

29.03.2023

пт рентннтрр

Объяснение:

нтне

4,7(20 оценок)

Ответ:

lalka137

29.03.2023

Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии не больше данного от данной точки. Поверхность шара называется сферой.

Сфера - поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Уравнение сферы на картинке

2. Изобразим схематически шар и диаметр АВ сечения, проведенного под углом 45° к его радиусу.

Треугольник АОВ - равнобедренный прямоугольный, и его гипотенуза ( диаметр сечения) равна 8√2

Радиус сечения вдвое меньше =4√2

Сечение шара плоскостью - круг.

Площадь круга

S=πr²

Площадь сечения = π (4√2)² =32 см²

3. Проводим ВВ₁ || OO₁

Треугольник АВВ₁ - прямоугольный

АВ₁=8 ( по теореме Пифагора) или потому то это египетский треугольник

АВ₁²=АВ²-ВВ₁²=10²-6²=64=8²

Рассмотрим треугольник АОВ₁ ( см рисунок справа)

Равнобедренный треугольник. проведем высоту ОК. По теореме Пифагора

ОК=3.

Или потому что треугольник АОК - египетский

ОК- расстояние между плоскостью, содержащей отрезок АВ и плоскостью, содержащей ось ОО₁

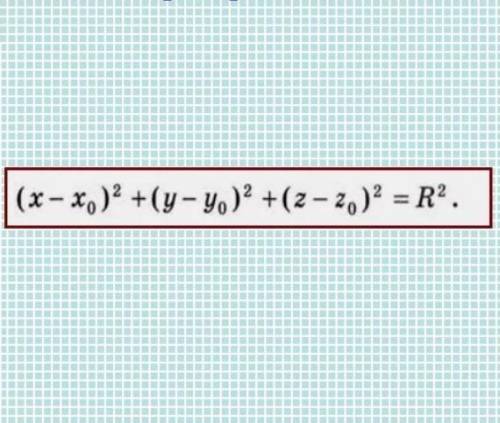
1. Объясните, какая поверхность называется сферой и какое тело называется шаром. Выведите уравнение

4,4(7 оценок)

Открыть все ответы

Ответ:

notix55

29.03.2023

Объяснение:

Если диагональ образует с площадью основания,то диагональ основания равна высоте прямоугольного параллелепипеда.

Найдём диагональ основания по теореме Пифагора:

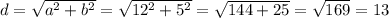
$d=\sqrt{a^{2} +b^{2} } =\sqrt{12^{2}+5^{2} } =\sqrt{144+25} =\sqrt{169} =13$

h=d=13 см

S = 2(a · b + a · h + b · h)=2(12 · 5 + 12 · 13 + 5 · 13) =2(60+156+65) = =2*281=562 см²

V=a · b · h=12 · 5 · 13=780 см³

Если образующая конуса наклонена к плоскости основания на 45°,то радиус основания равен высоте.Примем радиус основания за х,тогда по теореме Пифагора:

l²=2r²

12²=2x²

x²=144:2

x²=72

x=√72=6√2 см

S=π r (r + l)=π6√2(6√2+12)=π72+π72√2=π72(1+√2) см²

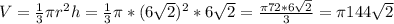
$V=\frac{1}{3} \pi r^{2}h=\frac{1}{3} \pi *(6\sqrt{2})^{2} *6\sqrt{2} =\frac{\pi 72*6\sqrt{2} }{3}= \pi 144\sqrt{2}$

V=144√2 π см³

4,5(41 оценок)

Ответ:

IlyaLS

29.03.2023

См. решение

Объяснение:

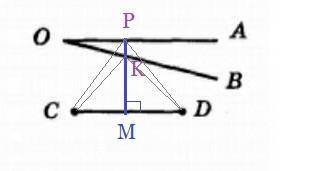
1) Находим середину отрезка CD и отмечаем ее точкой M

2) Через точку M строим перпендикуляр к отрезку CD. Отмечаем точки пересечения перпендикуляра со сторонами <AOB: P и K

3) Докажем что точки P и K равноудалены от C и D.

Рассмотрим ΔCMK и ΔDMK: <CMK = 90° = <DMK, CM = MD по условию, MK - общая сторона для ΔCMK и ΔDMK, => ΔCMK = ΔDMK по двум катетам, => CK = KD, т.е точка K - равноудалена от C и D и точка K лежит на стороне OB <AOB

Аналогично рассмотрим ΔCMP и ΔDMP: <CMP = 90° = <DMP, CM = MD по условию, MP - общая сторона для ΔCMP и ΔDMP, => ΔCMP = ΔDMP по двум катетам, => CP = PD, т.е точка P - равноудалена от C и D и точка P лежит на стороне OA <AOB