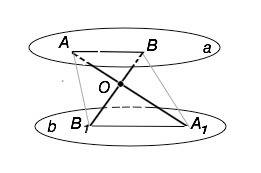
Пусть А и В лежат в плоскости а, А1 и В1 – в плоскости b.
АА1 и ВВ1 пересекаются.
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
Плоскости а и b параллельны, плоскость АВА1В1 пересекает их.
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.⇒
а)
АВ ║А1В1
б)
В ∆ АОВ и ∆ А1ОВ1 накрестлежащие углы равны, углы при О равны.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. ⇒
∆ АОВ и ∆ А1ОВ1 подобны.
Коэффициент подобия k=АО:ОА1=3:5 ⇒
АВ:А1В1=3:5
3А1В1=5АВ
А1В1=5•18:3=30 см
Объяснение:
Y=1/4x^2+1
Y=1/4•(-2)^2+1
Y=1/4•4+1
Y= 4/4+1
Y=1+1
Y=2