
Диаметр AK стягивает дугу 180°.
∪AK=180°
Вписанный угол равен половине дуги, на которую опирается.
∠CAK=20° => ∪CK=40°
Точки A и С делят окружность на две дуги:
∪AC =∪AK -∪CK =180° -40° =140°
∪AC'=∪AK' +∪CK =180° +40° =220°
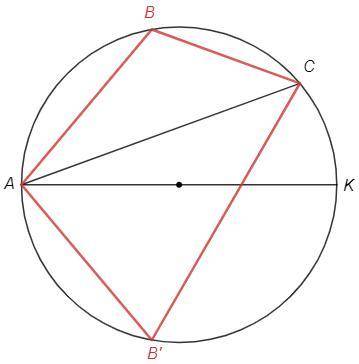
Точка B может лежать на одной из двух дуг (угол BCA может быть отложен в одну из двух полуплоскостей).
Соответственно, вписанный угол ABC опирается на одну из двух дуг и равен половине ∪AC или половине ∪AC'.
∠ABC =∪AC/2 =70°
или
∠ABC =∪AC'/2 =110°
Величина угла между плоскостями – угол, сторонами которого являются лучи, по которым эти плоскости пересекаются плоскостью, перпендикулярной ребру угла.
Искомый угол –это угол DHC, образованный отрезками СН и DH (см. рисунок в приложении).
СН - высота ∆ АВС, DC –⊥ плоскости ∆ АВС по условию, DH ⊥ АВ по т. о трёх перпендикулярах,
плоскость DHC перпендикулярна АВ.
СН как катет ∆ АНС, противолежащий углу 30º, равен половине гипотенузы АС и равен а/2
Тангенс угла DHC=DC/HC=[(а√3):2]:a/2=√3.
Это тангенс угла, равного 60º.
Угол между плоскостью (ADB) и плоскостью (ACB)=60º.
Объяснение:
Объяснение:
∠АВС = 1/2 дуги АС = 1/2 (180 - дуга КС) = 1/2 * 140 = 70°