1. В
2. В
3. А
4.б
5. а
6.б
7.в
8.в
9.в
10.а
11.в
Две окружности ,вписанные в угол ,касаются друг друга внешним образом .Центральный угол в 120° большей окружности , составленный из радиусов проведенных в точки касания ,стягивает дугу 15 см. Найти длину малой окружности.
Объяснение:
Пусть ОА=ОМ=R , CM=CK=r . По формуле длины дуги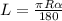 
,
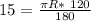⇒ R=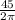 
см. По свойству отрезков касательных ∠АОР=60° .
Пусть СН⊥ОА , тогда ∠НСО=30°.
В ΔНСО по свойству угла 30° : ОС=2*ОН , но ОС=R+r , ОН=R-r ,
тогда R+r=2(R-r) → r=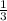 
*R → r= 
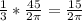(см) .
Длина окружности С=2πr , тогда С=2π*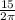 
=15 (см) .
Объяснение:
4.а) 50°
х вписанный угол,равен половине центрального, опирающегося на общую дугу.
х=100°/2=50°
5. в) 110°
свойство четырех угольник вписанного в окружность: сумма противолежащих углов =180°
х=180°-70°=110°
6. б) 32°
х вписанный угол, равен половине соответствующего центрального
х= 64°/2=32°
7. в) 60°
угол АВО =90° (свойство касательной к радиусу)
ВА=АС(касательные из одной точки)
треугольники ВАО и ОАС равны по двум сторонам и углу между ними
ВO=DO(радиусы)
ВО=DO=DA
BO=OA/2
OA гипотенуза
свойство угла 30°: катет лежащий против угла 30° равен половине гипотенузы
угол ВАО=30°
угол ВАС=30°*2=60°
1)a
2)a
3)б
4)в
5)в
6)а
7)б
8)в
9)б
10)а
11)а
Объяснение:
Мы тоже делали эту всё правильно