Задача решена Пользователем Рисадес Хорошист
Исправлена неточность в последнем действии.
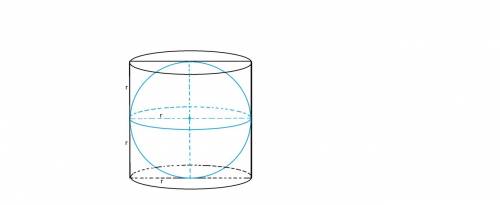
Шар может быть вписан в цилиндр только тогда, когда этот цилиндр правильный, т.е. когда его осевое сечение является квадратом.
Радиус основания цилиндра равен радиусу шара и равен r.
Высота цилиндра равна диаметру основания и равна 2 r.
Полная площадь поверхности складывается из площади двух оснований и площади боковой поверхности:
2*πr² + 2πr*2r = 6πr²
Площадь шара = 4πr²
Площадь цилиндра больше площади шара в
6πr² : 4πr² = 1,5 (раза)
Площадь полной поверхности шара
111 : 1,5 = 74 ( единиц площади)
1)При вращении прямоугольника вокруг большей стороны получается цилиндр с радиусом R, равной большей стороне, и высотой Н, равной меньшей стороне
R = 10см
H = 6см
Объём цилиндра
V = πR²·H = π·100·6 = 600π;
2)С - площадь основания пирамиды. ;
Ш-высота пирамиды ;
В - объем пирамиды ;
Л- апофема ;
а - угол между апофемой и высотой;
син - синус ;
кос - косинус ;
тан - тангенс ;
кор - корень из ;
кв. - в квадрате ;
кб. - в кубе ;
С=0.5 *(2*Л*син(а)/тан(30))*(2*Л*син(а)*кос(30)/тан(30))=
= Лкв.*синкв.(а)/кор(3) ;
Ш= Л*кос(а) ;
В=С*Ш/3=Лкб.*синкв(а)*кос(а)/(3*кор(3)).
3)извини((третье не знаю(