Знайдіть основу рівнобедреного трикутника, в якому бічна сторона і медіана,проведена до неї, відповідно дорівнюють 8см, 6 см !
Найдите основание равнобедренного треугольника, в котором боковая сторона и медиана, проведенная к ней, соответственно равны 8 см, 6 см .
Дано: ΔABC
с = BA = ВC = a =8 см, BM =CM =BС/2 ; AM = mₐ =6 см . - - - - - - - AС =b - ?
ответ: 2√10 см
Объяснение:
ΔABC : AC² = BC² + BA² - 2BC*BA*cos∠B
b² = a² + c² - 2ac*cos∠B =2a²( 1 -cos∠B )
cos∠B нетрудно определить из ΔABM заданной по трем сторонам. AM² = BA²+BM² - 2BA*BM*cos∠B ⇔
mₐ² = c² + (a/2)² - ca*cos∠B = a²/4+ a²(1- cos∠B ) ⇒
a²(1- cos∠B ) = mₐ² - a²/4 ;
b² =2a²( 1 - cos∠B ) =2(mₐ² - a²/4 ) =2(6²-8²/4) =2*20 =40
b = √40 =2√10 (см)
2-ой
обозначаем ∠AMB = φ ⇒ ∠AMC = 180° - ∠AMB = 180° - φ
ΔAMB : c² = mₐ² + (a/2)² - 2mₐ*(a/2) cosφ
ΔAMC : b² = mₐ² + (a/2)² - 2mₐ*(a/2)cos(180° - φ) ; [ cos(180°- φ) = - cosφ ]
c² + b² = 2mₐ² + a²/2 [ c = a ] b² = 2mₐ² - a²/2
* * * mₐ = 0,5√( (2(b²+c²) -a² ) _формула для вычисления медианы * * *
b² = 2*6² - 8²/2 = 40
b =√40 = 2√10 (см )
* * * * * * * * * * * * *
Построить треугольник по двум сторонам и медиане , проведенной к третей стороне
Объяснение:
1)
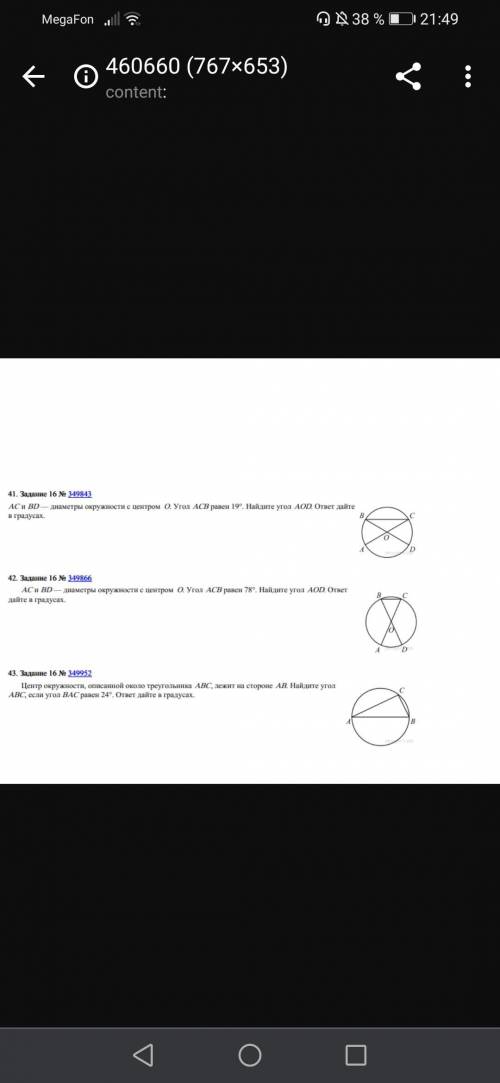
<ACB=<CBD, ∆ВОС- равнобедренный, ВО=ОС=R
Сумма углов в треугольнике равна 180°
<ВОС=180°-<ОСВ-<СВО=180°-2*19°=142°
<ВОС=<АОD, вертикальные углы.
ответ: <АOD=142°
2)
<B=<C, ∆OBC- равнобедренный ВО=ОС=R
Сумма углов в треугольнике равна 180°
<BOC=180°-<B-<C=180°-78°-78°=24°
<ВОС=<АОD, вертикальные углы.
ответ: <АОD=24°
3)
∆ACB- прямоугольный треугольник
<С=90°, АВ- диаметр окружности.
Сумма острых углов в прямоугольном треугольнике равна 90°
<А+<В=90°
<В=90°-<А=90°-24°=66°
ответ: <АВС=66°