1)
Если трапеция равнобедренная, то АБ=СД=5, следовательно АБ+СД=10.
Тогда сумма двух оснований равна 32-10=22.
Площадь равна средняя линия * h(высоту)
Ср линия = 22/2=11.
Из формулы площади найдем высоту:
h=S/ср.лин
следовательно высота равна 44/11=4
ответ: h=4
2)
S(трапецииABCD) = (AD + BC) : 2 * h
h - высота трапеции и треугольника ACD
S(ACD) = 1/2 * AD * h, следовательно
h = S(ACD) / (1/2 * AD) = 30 / (1/2 * 10) = 30 : 5 = 6 см
S(трапецииABCD) = 1/2*(10 + 8) * 6 = 9 * 6 = 54 см²
P.S. 1/2 - 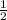
/ - дробь
МР-средняя линия треугольника АВС, тогда отношение площади треугольника АМР к площади АВС равно квадрату коэффициента подобия (1/2)квадрат=1/4. То есть Sамр=Sавс/4=24/4=6. Медиана МС делит треугольник АВС на два равновеликих, то есть Sамс=Sавс/2=24/2=12. Тогда Sмрс=12-Sамр=6. МРQC-параллелограмм поскольку МQ и МР-средние линии, но по условию половины его диагоналей равны ОР=ОС=2,5 следовательно это прямоугольник. Стороны треугольника АМР равны средним линиям треугольника АВС. Смотри рисунок.