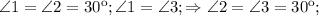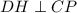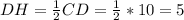) 
, 
как катет лежащий против угла 30 в треугольнике CHD. 
, 
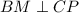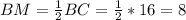как катет лежащий против угла 30 в треугольнике BMC.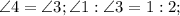 
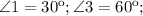Тогда в ромбе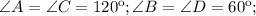 
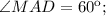, тогда 
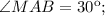Треугольник BAM равнобедренный, АВ=АМ, тогда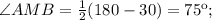 
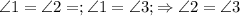, треугольник MCD равнобедренный, MD=CD=3, 
, 
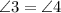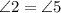, как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4.
.
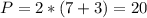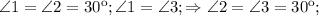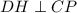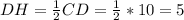) , как катет лежащий против угла 30 в треугольнике CHD. 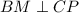, 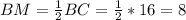как катет лежащий против угла 30 в треугольнике BMC.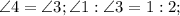 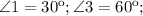Тогда в ромбе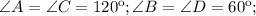 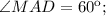, тогда 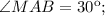Треугольник BAM равнобедренный, АВ=АМ, тогда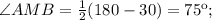 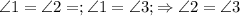, треугольник MCD равнобедренный, MD=CD=3, 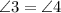, , 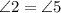как накрест лежащие при параллельных прямых АВ и CD, треугольник NAM равнобедренный, AM=AN=4..
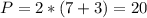ответ: 2*x+y+2=0.
Объяснение:
Будем искать уравнение прямой в виде y-y0=k1*(x-x0), где x0=0 и y0=-2 - координаты точки, через которую проходит прямая, k1 - неизвестный пока угловой коэффициент этой прямой. Составим уравнение прямой, проходящей через точки (0;-3) и (4;-1): (x-0)/(4-0)=(y+3)/(-1+3), или x/4=(y+3)/2, или y=0,5*x-3. Угловой коэффициент этой прямой k2=0,5, отсюда - так как прямые перпендикулярны - k1=-1/k2=-2. Поэтому искомое уравнение имеет вид y+2=-2*x, или 2*x+y+2=0.