Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Пусть дан отрезок ВС.
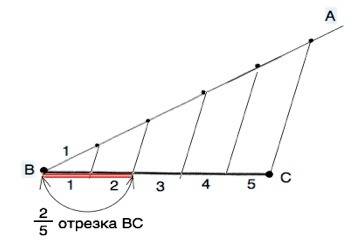
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
Опускаем высоты ВК и СМ из точек В и С. АК=х, тогда КМ=7,5, МД=17,5-7,5-х=10-х.
Решаем два прямоугольных треугольника по теореме Пифагора относительно высоты. 64-х^2= 36- (10-x)^2
64-x^2= 36-100+20x-x^2
20x=128
x=6,4
Высота ВК = корень из (64-6,4^2)= 4,8 см.
Площадь трапеции равна произведению полусуммы оснований на высоту = (7,5+17,5):2*4,8 = 60 квсм.