Сумма острых углов прямоугольного треугольника равна 90°
=> ∠А = 90 - 45 = 45°
Так как ∠А = ∠М = 45° => ∆АВМ - равнобедренный.
=> АВ = ВМ = 22, по свойству.
ВМ - расстояние от M до АВ.
ответ: 22.
Задача #3.Решение (1 часть):
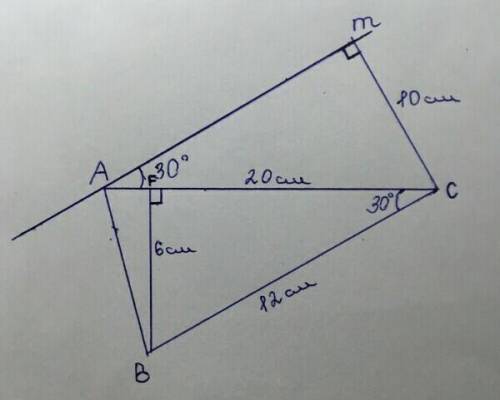
Проведём перпендикуляр BF от В до АС (он же высота)
Получился ∆BFC - прямоугольный.
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> BF = 12 ÷ 2 = 6 см.
ответ: 6 см (расстояние от В до АС).
Решение (2 часть):
При пересечении двух параллельных прямых секущей накрест лежащие углы равны.
Так как m || BC => ∠МАС = ∠С = 30°, как накрест лежащие.
Проведём перпендикуляр от m к точке С
Получился ∆МСА - прямоугольный.
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> МС = 20 ÷ 2 = 10 см.
ответ: 10 см (расстояние от прямой m до прямой ВС).
120
Объяснение:
треугольники EBF=FCM=MDN=NAE (углы прямые , а стороны равны по условию). Следовательно EF=FM=MN=EN.
ABCD - прямоугольник, треугольник ACD прямоугольный, с углами 60 и 30. AD= CD/ctg60=30√3
AN=ND=30√3/2=15√3
CM=MD=30/2=15
Рассмотрим прямоугольный треугольник NMD. Найдем гипотенузу MN по теореме Пифагора:
МN^2= 675+225=900
MN=30
P(EFMN)= 30*4=120