1. 84°, 84°, 96°, 96°
2. Стороны: 1 см, 1 см, 2,5 см, 2,5 см
Углы: 42°, 42°, 138°, 138°
Объяснение:
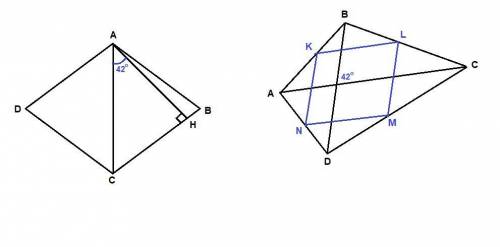
1. Рассмотрим прямоугольный треугольник АСН.
Сумма острых углов равна 90°, тогда\
∠АСН = 90° - ∠САН = 90° - 42° = 48°
Диагонали ромба лежат на биссектрисах его углов, поэтому
∠BCD = 2∠АСН = 2 · 48° = 96°
Сумма соседних углов параллелограмма равна 180°:
∠CDA = 180° - ∠BCD = 180° - 96° = 84°
Противолежащие углы ромба равны:
∠АВС = ∠CDA = 84°
∠BAD = ∠BCD = 96°
2. ABCD - данный четырехугольник,
АС = 5 см, BD = 2 см.
Точки К, L, M, N - середины соответствующих сторон.
Найти углы и стороны четырехугольника KLMN.
KL - средняя линия ΔАВС, ⇒
KL║AC, KL = AC/2 = 2,5 см
MN - средняя линия ΔADC, ⇒
MN║AC, MN = AC/2 = 2,5 см
Так как противолежащие стороны четырехугольника параллельны и равны, то это параллелограмм (по признаку параллелограмма).
Аналогично,
KN - средняя линия ΔABD, ⇒
KN║BD, KN = BD/2 = 1 см
LM - средняя линия ΔBCD, ⇒
LM║BD, LM = BD/2 = 1 см.
Так как стороны параллелограмма KLMN параллельны диагоналям четырехугольника АВСD, то угол между сторонами будет равен углу между диагоналями:
∠KLM = 42°
Сумма соседних углов параллелограмма равна 180°, поэтому
∠LKN = 180° - 42° = 138°
Противолежащие углы параллелограмма равны:
∠KNM = ∠KLM = 42°
∠LMN = ∠LKN = 138°
Треугольник существует, если а+b>c
a+c>b
c+b>a.
a+b=5,38+0,46=5,84
5,84>c
5,38+c>0,46
c+0,46>5,38
Предположим с=5:
5,84>5
5,38+5>0,46
5+0,46>5,38
условия выполняются, значит ответ: с=5.
(если возьмём следующее целое число (6), то условия не будут выполняться (5,84 не больше 6) следовательно такой треугольник не существует. Возьмем меньшее целое число (4), условия не выполняются (4+0,46 не больше 5,38), значит треугольник не существует).
ответ:5.