2. У AKCN: 2C = 90°; CA I KN; KA = 16 см; AN = = 4 см. Знайти: KN; AC; СК; СК?; CN?. . - id1690608620200713 от sonyavolkova26 13.07.2020 23:49

Question

Геометрия: 2. У AKCN: 2C = 90°; CA I KN; KA = 16 см; AN = = 4 см. Знайти: KN; AC; СК; СК?; CN?. .​

sonyavolkova26 · Accepted Answer

Найдём расстояния между точками, это и будут стороны треугольника.

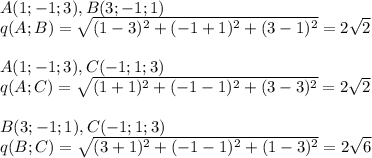
$A(1;-1;3),B(3;-1;1)\\q(A;B)=\sqrt{(1-3)^2+(-1+1)^2+(3-1)^2}=2\sqrt{2}\\\\A(1;-1;3),C(-1;1;3)\\q(A;C)=\sqrt{(1+1)^2+(-1-1)^2+(3-3)^2}=2\sqrt{2}\\\\B(3;-1;1),C(-1;1;3)\\q(B;C)=\sqrt{(3+1)^2+(-1-1)^2+(1-3)^2}=2\sqrt{6}$

Три точки всегда лежат только в одной плоскости, задача свелась к обычной планиметрии, мы знаем три стороны треугольника. Надо найти углы, периметр и площадь.

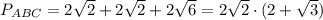
$P_{ABC}=2\sqrt{2}+2\sqrt{2}+2\sqrt{6}=2\sqrt{2}\cdot (2+\sqrt{3})$

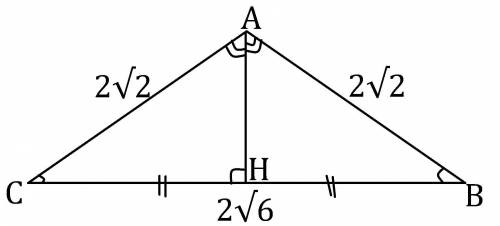
H∈BC; AH⊥BC; ΔABC - равнобедренный, поэтому высота будет и медианой, и биссектрисой.

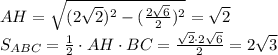
$AH=\sqrt{(2\sqrt{2})^2-(\frac{2\sqrt{6}}{2})^2}=\sqrt{2}\\S_{ABC}=\frac{1}{2}\cdot AH\cdot BC=\frac{\sqrt2\cdot 2\sqrt6}{2}=2\sqrt{3}$

В прямоугольном ΔAHC, катет AH в два раза меньше гипотенузы AC, поэтому угол лежащий напротив катета AH равен 30°, то есть ∠С = 30°.

∠B = ∠C = 30°. ∠A = 180° - 30° - 30° = 120°.

ответ: ∠A = 120°; ∠B = 30°; ∠C = 30°;

Периметр: 2√2 · (2+√3);

Площадь: 2√3.

Решите с пояснениями: найдите углы,периметр и площадь треугольника,вершинами которого являются точки

2. У AKCN: 2C = 90°; CA I KN; KA = 16 см; AN == 4 см.Знайти: KN; AC; СК;СК?; CN?. .​

MOGZ ответил

2. У AKCN: 2C = 90°; CA I KN; KA = 16 см; AN =
= 4 см.
Знайти: KN; AC; СК;
СК?; CN?. .