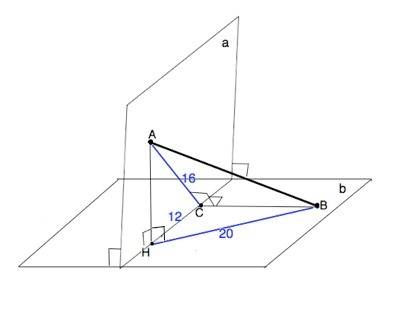
Пусть данные плоскости а и b.
А ∈ а, В ∈ b.
АН⊥СН, ВС⊥СН
ВН - проекция АВ на плоскость b,
АС - проекция АВ на плоскость а.
∆ АСН - прямоугольный, ∠АНС=90°
По т.Пифагора АН²=АС²-СН²=256-144=112
АН перпендикулярен линии пересечения взаимно перпендикулярных плоскостей, следовательно, АН перпендикулярен любой прямой, лежащей в плоскости b и проходящей через Н.
∆ АНВ - прямоугольный. ∠АНВ=90°
По т.Пифагора АВ²=АН²+ВН²=512
АВ=√512=16√2
Или:
∆ СНВ - прямоугольный, ∠ВСН=90° ⇒
По т.Пифагора СВ²=ВН²-СН²=400-144=256
ВС=√256=16
∆ АСВ- прямоугольный. ∠АСВ=90°
По т.Пифагора АВ² = АС² +ВС² =256+256=512⇒
АВ=√512=16√2
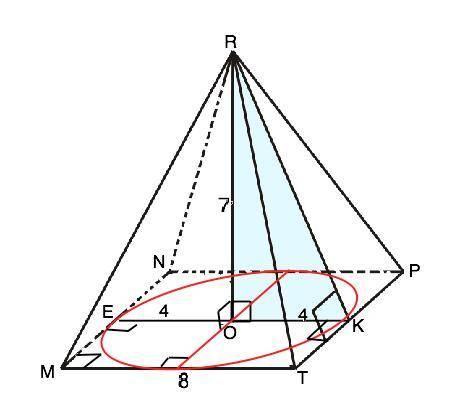
Апофемой правильной пирамиды называется высота боковой грани, проведенная из вершины пирамиды.
Основание правильной четырехугольной пирамиды - правильный четырёхугольник (квадрат), боковые грани - равнобедренные треугольники. Высота правильной четырехугольной пирамиды проецируется в точку пересечения диагоналей квадрата (основания), иначе – в центр вписанной в основание окружности.
Диаметр вписанной в квадрат окружности равен длине его стороны и перпендикулярен сторонам в точках касания. ⇒ ЕК=8, ЕК⊥РТ, ∆ ROK - прямоугольный. ОК=ОЕ=8:2=4. По т.Пифагора апофема RK=√(RO²+OK²)=√(7²+4²)=√65 (ед. длины)
0,13 м = 1,3 дм
0,73 м = 3,7 дм
Дана трапеция ABCD, у которой известны все стороны. Нужно найти высоту, чтобы вычислить площадь.
Проведем отрезок BE к нижнему основанию AD параллельно боковой стороне трапеции CD. Поскольку BE и CD параллельны и проведены между параллельными основаниями трапеции BC и DA, то BCDE - параллелограмм, и его противоположные стороны BE и CD равны. BE=CD.
Рассмотрите треугольник ABE. AE=AD-ED. Основания трапеции BC и AD известны, а в параллелограмме BCDE противолежащие стороны ED и BC равны. ED=BC, значит, AE=AD-BC.
Теперь найдем площадь треугольника ABE по формуле Герона (вложение 2).
p = 4,5
S = 2,4
Найдем высоту
ВО = 2S / AE
BO = 0,6
Высота треугольник является и высотой трапеции.
Sтрап = (2+6)*0,6 / 2 = 2,4 дм