ответ: 2√37 см
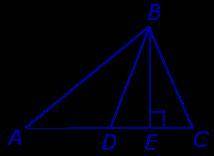
Объяснение: Дано: ΔАВС, АВ=15 см, АС=14 см, ВС=13 см, BD-медиана AD=CD. Найти BD
1) По формуле Герона найдем площадь треугольника
S=√(p(p-a)(p-b)(p-c)) где p-полупериметр
p=13+14+15):2=21
S=√(21(21-13)(21-14)(21-15))=√7056=84
Мы также знаем что S треугольника=1/2а•h возьмем среднюю сторону за основание, проведём высоту h=ВЕ
84=1/2•14• ВЕ ⇒ ВЕ=12 см
2)Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (см рис). ⇒AD=CD=14:2=7 см. На нашем рисунке медианой является отрезок BD.
3) Из прямоугольного ΔВЕС по теореме Пифагора:
CE²=BC²-BE²=13²-12²=169-144=25, ⇒CE=5 см
Тогда DE=CD-CE= 7-5=2 см
4) Из прямоугольного ΔВЕD по теореме Пифагора:
BD²=DE²+BE²=2²+12²=4+144=148 ⇒ BD=√148=2√37 см
В ΔАВС:АС=2*2=4(см)(гипотенуза=удвоенному катету,лежащему напротив
угла 30 градусов)
ВС²=АС²-АВ² ⇒ВС=√4²-2²=2√3(см).
Sосн=1/2*АВ*СВ=1/2*2*2√3=2√3(см²).
Sбок=Р*Н=(2+4+2√3)*2√3=12√3+12=12(√3 +1)(см²).
1) Sполн=2Sосн+Sбок=2*2√3+12(√3 +1)=4√3+12√3+12=16√3+12(см²).
2) ПлоскостьА1ВC-тр-к,уголА1ВС=90 градусов(теорема о трех перпендикулярах)
SΔ=1/2А1В*ВС; из ΔА1АВ найдем A1B : A1B²=АА1²+АВ²;
A1B=√(2√3)²+2²=√12+4=√16=4(см).
SΔА1ВС=1/2*4*2√3=4√3(см²).
3) Двугранный угол между плоскостямиА1ВС иАВС лежит в плоскости,перпендикулярной ВС.(плоскостьАА1В1В) это уголА1ВА.=α
tgα=2√3/2=√3 ⇒α=60 градусов.
4) СС1 параллельнаВВ1.гол между прямой плоскостью ищем в плоскостиАА1ВВ1,1ВС.Это уголА1ВВ1.
уголА1ВВ1.=90-α=90-60=30(градусов).
5) АВ1 лежит в плоскости,перпендикулярной А1ВС.(По теореме о трех перпендику
лярах),значит,и плоскость перпендикулярна А1ВС.
основание 3.5 ,т.к. катет лежащий против угла в 30 градусов равен половине гипотенузы , 3.5 * 7 /2 = 12.25