
остроугольный и равнобедренный.
Объяснение:
Если боковые рёбра пирамиды составляют равные углы с плоскостью основания, то основанием высоты пирамиды является центр окружности описанной около многоугольника из основания.
Центр окружности описанной около треугольника лежит внутри треугольника, если он остроугольный.
Так же этот центр лежит на пересечении серединных перпендикуляров к сторонам треугольника. Если центр описанной окружности лежит на одной высоте треугольника, то эта высота лежит на серединном перпендикуляре. А значит высота одновременно является и медианой. Тогда треугольник равнобедренный.
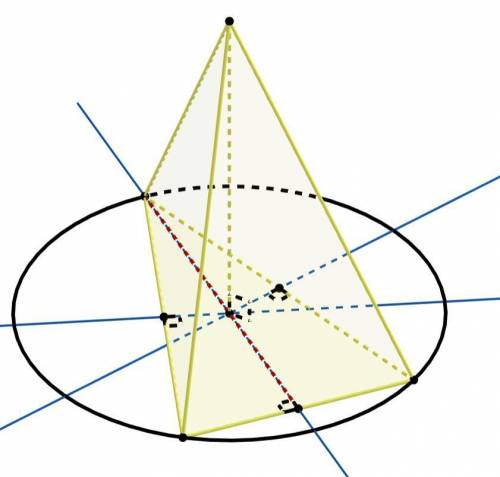
Объяснение:
2. 1.) Пускай гипотенуза это АВ, а катет 4 см это ВС. Тогда мы имеем египетский треугольник. То есть треугольник со сторонами 3 см, 4 см и 5 см. Значит катет СА равен 3 см.
2.) S = 1\2 * СА * ВС = 1\2 * 4 * 3 = 6 с
ответ: S = 6 с
3.
1.) Пускай стороны АВ и ВС это х. Тогда имеем уравнение:
х + х + 14 = 64
2х = 64 - 14
2х = 50
х = 25 см - стороны АВ и ВС
2.) Проведем висоту с вершини угла В на основание АС и назовем её ЕВ. Висота делит основание АС на две равные части т.к в равнобедренном треугольнике висота есть и биссектрисой и медианой. От сюда выпливает что АЕ = ЕС = 7 см Тогда за метрическими соотношениями имеем, что
Е = АЕ * ЕС
ЕВ = √ AE * EC =√ 7 * 7 = √49 = 7 cм
3. Значит площадь равна:
S = 1\2 * AC * ВЕ = 1\2 * 7 * 14 = 1\2 * 98 = 49 сv²
ответ: S = 49 см²