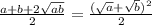
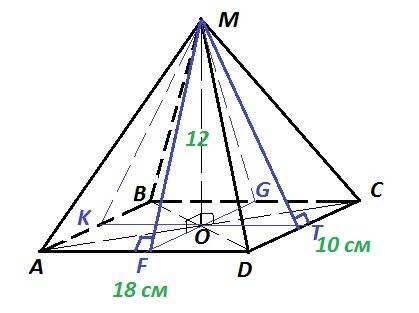
Пирамида MABCD, основание - прямоугольник ABCD: AD=BC=18 см; AB=CD=10 см; O- точка пересечения диагоналей AС и BD, MO - высота пирамиды.
Так как у прямоугольника диагонали равны и точкой пересечения делятся пополам, то OA = OB = OC = OD - это проекции боковых ребер на основание. Проекции наклонных равны, следовательно, наклонные тоже равны : AM = BM = CM = DM - боковые ребра пирамиды. Тогда ΔAMD = ΔBMC - по трём равным сторонам, ΔAMB = ΔDMC - по трём равным сторонам.
Проведем KT║AD ⇒ OK=OT=AD/2 = 18/2 = 9 см
ΔMOT - прямоугольный, теорема Пифагора
MT² = MO² + OT² = 12² + 9² = 144+81=225 = 15²
MT = 15 см
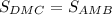
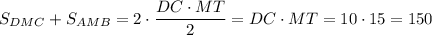 см²
см²
Проведем FG║DC ⇒ OG=OF=DC/2 = 10/2 = 5 см
ΔMOF - прямоугольный, теорема Пифагора
MF² = MO² + OF² = 12² + 5² = 144+25 = 169 = 13²
MF = 13 см
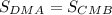
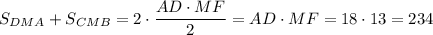 см²
см²
Площадь боковой поверхности пирамиды
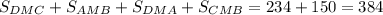 см²
см²
Sбок = 384 см²
Площадь основания
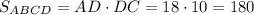 см²
см²
Площадь полной поверхности пирамиды
S = 384 + 180 = 564 см²
Пусть сторона куба "а".
Совместим с кубом систему координат: А(0;0;0) - начало координат
ось X вдоль стороны АД; ось Y вдоль стороны АВ; ось Z вдоль стороны АА1.
Тогда координаты вершин будут иметь значения:
А(0;0;0); В(0;а;0); С(а;а;0); D(а;0;0); А1(0;0;а); В1(0;а;а); С1(а;а;а); D1(а;0;а);
вектор AB1 = {0; a; a}
вектор ВD1 = {a; -a; a}
Скалярное произведение этих векторов = 0*а + а * (-а) + а*а = 0
Так как скалярное произведение =0, то векторы перпендикулярны друг другу и угол между ними 90 градусов.
Отв. 90 градусов.