Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 3см 4см. Найдите радиус круга, вписанного в треугольник
Объяснение:
Пусть один катет а, другой катет b. . По т. о биссектрисе треугольника
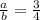, тогда а= 
.
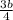По т. Пифагора а²+b²=(3+4)² ,( 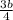)²+b²=49 ,
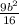+b²=49 , 9b²+16b²=49*16 , b²= 
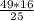, b=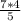
= 5,6 (см)
a=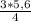 
=4,2 cм
S=1/2*Р*r . Найдем площадь прямоугольного треугольника
S=1/2*5,6*4,2=1/2*23,52 (см²) . Найдем периметр Р=16,8 см. Тогда
1/2*23,52=1/2*16,8*r , r= 23,52/16,8 , r=1,4 см
===============================
Теорема о биссектрисе треугольника " Биссектриса треугольника делит противоположную сторону на два отрезка, длины которых относятся так же, как длины соответствующих сторон."
т.к. AD--боковая сторона, то АВ и CD -- основания, CL || AB || CD и получилось, что CL||CD и у этих прямых есть общая точка С ((они пересекаются)))
итак, AD --основание...
AL=LD=BC, т.к. в параллелограмме противоположные стороны равны...
из известной площади трапеции можно найти высоту...
S = (BC+AD)*h/2 = 90
(BC+AD)*h = 180
h = 180 / (BC+AL+LD) = 180 / (3*BC) = 60 / BC
S(ABCL) = h*BC = 60*BC/BC = 60
можно и иначе порассуждать:
диагональ параллелограмма АС разбивает параллелограмм на 2 равных треугольника -- S(ABC)=S(ACL)
а медиана CL разбивает треугольник АСD на 2 РАВНОВЕЛИКИХ
(но НЕ равных---т.е. равных по площади))) треугольника S(ACL)=S(CLD)
получили, что вся трапеция разбивается на 3 равных по площади треугольника)))
а площадь параллелограмма = двум площадям таких треугольников...
90*2/3 = 30*2 = 60