Пусть у нас есть квадрат ABCD
и прямоугольник EBFG. Вершины B прямоугольника и квадрата совпадают. Сразу оговоримся, что именование вершин фигур начинается с левого верхнего угла и продолжается по порядку по часовой стрелке.
Нам известно что AB = BC = CD = DA = 10 см., EB = FG = 3см., BF = GE = 4 см.
Тогда от сюда следует что новая фигура, образовавшаяся после выреза прямоугольника (AEGFCD) будет иметь следующие размеры:
AE = AB - EB = 10 - 3 = 7см.
EG = GE = 4 см.
GF = FG = 3 см.
FC = BC - BF = 10 - 4 = 6 см.
CD = 10 см.
DA = 10 см.
Ссумируем 7 + 4 + 3 + 6 + 10 + 10 = 40 см.
ответ 40 см.
ответ: 1200π
Объяснение:
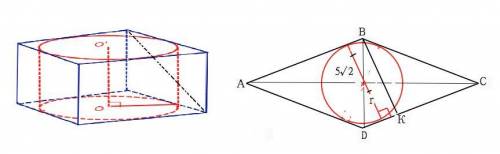
Формула объёма прямой призмы V=S•H, где Ѕ - площадь основания, Н - высота призмы.
Высота призмы равна высоте вписанного цилиндра, которая, в свою очередь, равна его оси. Ось цилиндра параллельна боковой грани призмы, диагональ боковой грани принадлежит её плоскости. Эти два отрезка не пересекаются и не параллельны - они скрещиваются. Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
Окружность основания цилиндра касается боковой грани призмы, радиус перпендикулярен стороне основания, поэтому расстояние между осью цилиндра и диагональю боковой грани призмы равно радиусу цилиндра.
Ѕ(полн. цил)=2Ѕ (осн)+Ѕ(бок).
Ѕ(осн)=πr²=π•(5√2)²=50π ⇒2S=100π
Ѕ(бок)=106π-100π=6π
Ѕ(бок)=2πr•H ⇒ H=6π:2π•5√2=0,3√2
Высота ВК основания (ромба) равна диаметру основания цилиндра=2r=10√2
Сторона ромба АВ=ВС=ВК:sin45°=(10√2•√2):2=20
S(ABCD)=AB•AC•BK=200•10√2=2000√2
V=π•2000√2•0,3√2=1200π
Фактически задача сводится к нахождению координат вектора CD.
Мы знаем, что СD перпендикулярно AB. И CD проходит через точку C.
Условие перпендикулярности -> косинус угла между векторами CD и AB равен нулю.
Формула косинуса угла между векторами - 
AB={-1+5;4-1}={4;3}
CD={x2-3;y2-2}
Составим уравнение прямой АВ: 
(*)
Подставляя вместо x1 и y1 в формулу косинуса 4 и 3 соответственно получим:
4(x2-3)+3(y2-2)=0
Также точка D принадлежит прямой AB, а значит x2 и y2 удовлетворяют уравнению (*).
Решаем полученную систему уравнений.
Мне лень решать - сами решите. Как найдёте x2 и y2 - подставьте их и найдите координаты вектора CD. Зная координаты направляющего вектора и точку, через которую проходит прямая, легко составить уравнение прямой.
Оно выглядит так: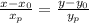 
, где 
- координаты напрвляющего вектора (в нашем случае вектора CD), а х0 и у0 - координаты точки, через которую проходит прямая (в нашем случае С или D - на выбор)
Слева нарисовать квадват, отметить его сторону 10см
а=10см
1)10*4=40cм
Р(маленький квадватик)=40см
Справа нарисовать приямоугольник, отметить его стороны.
а=4см
б=3см
2)2(4+3)=14
Р(малелький прямоуг.)=14см
Ниже:
3)40-12=28см
ответ: Р ост.фигуры=28см