Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника.
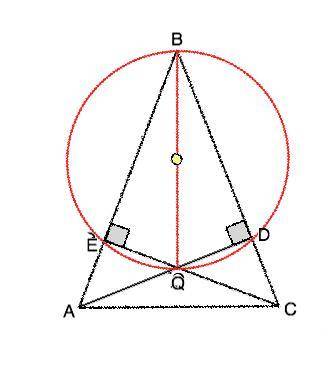
В четырехугольнике BEQD проведем диагональ ВQ, которая является общей гипотенузой треугольников DEQ и BDQ. Радиус окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы и равен её половине. Следовательно ,для прямоугольных треугольников ВEQ и BDQ описанная окружность будет общей и описанной около четырехугольника BEQD. Доказано.
* * *
Решение этой задачи может опираться на теорему о четырехугольнике, около которого описана окружность. Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность. Два противоположных угла прямые, их сумма 180°, следовательно, сумма ∠В+∠Q=180° ⇒ около четырехугольника BEQD можно описать окружность.
∠1 и ∠2 - накрест лежащие углы
∠1 = ∠2 ⇒ ∠1 + ∠2 = 2∠1 = 86°
∠1 = ∠2 = 86°/2 = 43°
ответ: 43°
Объяснение