
1) Прямая ОА пересекает окружность в двух точках, так как прямая бесконечна. Луч ОА пересекает окружность в одной точке, так как луч бесконечен в сторону точки А. Отрезок ОА не пересекает окружность, так как находится внутри нее.
2) Представим, что из точки на окружности К проведен радиус КОВ и хорда КС, равная радиусу. Проведем отрезок СО, который будет тоже являться радиусом окружности, и получим равносторонний треугольник КОС, в котором все стороны равны радиусу окружности. Все угла в равностороннем треугольнике равны 180/3=60 градусов.
Объяснение:
1) Прямая ОА пересекает окружность в двух точках, так как прямая бесконечна. Луч ОА пересекает окружность в одной точке, так как луч бесконечен в сторону точки А. Отрезок ОА не пересекает окружность, так как находится внутри нее.
2) Представим, что из точки на окружности К проведен радиус КОВ и хорда КС, равная радиусу. Проведем отрезок СО, который будет тоже являться радиусом окружности, и получим равносторонний треугольник КОС, в котором все стороны равны радиусу окружности. Все угла в равностороннем треугольнике равны 180/3=60 градусов.
Объяснение:
Відповідь:
Пояснення:
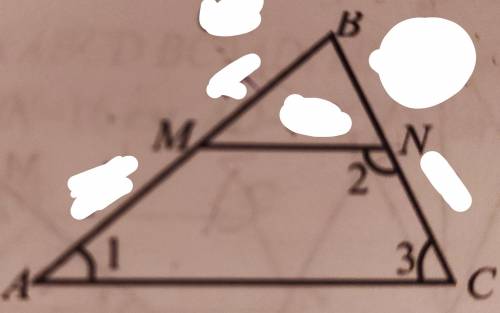
1. /_3+/_2=180°, как внутренние односторонние между паралельними прямими, учитивая, что /_3:/_2=1:2, имеем /_3=60°, /_2=120°
Так как /_1=30°, а /_3=60° →/_В=90°
Так как MN средняя линия, то ВС =2BN=8
По теореме синусов АС=ВС/sin30=16
АС+ВС=16+8=24
2.
Р△=AM+MN+NA=48
AB=2AM
AC=2MN
AB+AC=2(AM+MN)=54 → NA= 48 - 54/2=21
3.
AN+NX+2MN-(AM+MN+AN)=9
2MN+2NC=42 → MN + NC=21
AM=21-9=12
AB=2×21=24