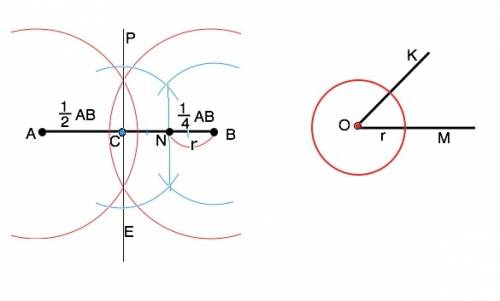
Обозначим данный отрезок АВ, а угол – КОМ. Для построение требуется:
1) разделить отрезок АВ пополам. Для этого равным раствором циркуля ( но больше половины отрезка АВ) из его концов, как из центров, чертим полуокружности. Прямая РЕ, проведенная через точки их пересечения, делит АВ пополам в точке С пересечения с ним ( и, заодно отметим и запомним,– перпендикулярно ему). 2) Аналогично разделить отрезок ВС пополам. Точка N - середина ВС, а отрезок ВN равен 1/4 отрезка АВ. 3) Из вершины О угла КОМ проводим окружность с радиусом r=ВN.
Все точки этой окружности удалены от вершины О угла КОМ на расстояние, равное ее радиусу, т.е. четверти данного отрезка Окружность - геометрическое место точек плоскости, расстояние от которых до центра окружности равно.
Если точка равноудалена от сторон треугольника, товысота оущенная из этой точки падает в центр впмсанной окружности, радус вычисляем по формуле (а+в-с)/2, где а и в - катеты с- гипотенуза. один катет известен -8, второй вычисляем по теореме пифагора
км=5 . радиус впмсанной окружности равен (12+5-13)/2=2
обозначим центр впмсанной окружности О, пусть окружность касается катета КМ в точке Д
треугольник АОД прямоугольный -АО перпендикуляр к плоскости треугольника - и есть искомое расстояние АД =8, ДО=2 По тореме пифагора находим
АО =√60=2√15