Диагонали прямоугольника равны и точкой пересечения делятся пополам.
Если один угол между диагоналями равен 120° , то второй, меньший, равен 60° как смежный с ним.
Треугольник, образованный двумя половинками диагоналей и меньшей стороной прямоугольника - равносторонний, так как он равнобедренный: две его стороны равны как половинки равных диагоналей, а угол при вершине равен 60° .
Следовательно, каждая половина диагонали равна 10 (меньшей стороное прямоугольника), а вся диагональ вдвое больше и равна 2*10=20.
т.к Δ АВС - прямоугольный 1) можно найти АВ по т. Пифагора:
АВ - гипотенуза АВ²=9+16=25
АС=3 см ⇒ АВ=5 см
СВ=4 см
угол С- прямой =90⁰
найти: АН-?
НВ-?
Высота СН -?
2)из св-ва прямоугольного треугольника( высота, опущенная из вершины прямого угла на гипотенузу, делит его на 2-а подобных Δ-ка, каждый из которых подобен данному тр-ку) т.е ΔАСН подобен ΔСВН СВ²=АВ*НВ (1)
ΔАСН подобен ΔАВС ⇒ АС²=АВ*АН (2) ⇒
ΔСВН подобен ΔАВС СН²=АН*ВН (3)
⇒ теперь подставляем (СВ=4, АВ=5) в (1)получаем 16=5*НВ
НВ=16/5=3,2
теперь подставляем во (2) (АС=3, АВ=5) получаем 9=5*АН
АН=9/5=1,8
и в (3) подставляем то что нашли и получаем: СН²= 1,8*3,2
СН=√5,76=2,4
ответ:АН=1,8 см; НВ=3,2 см; СН=2,4 см
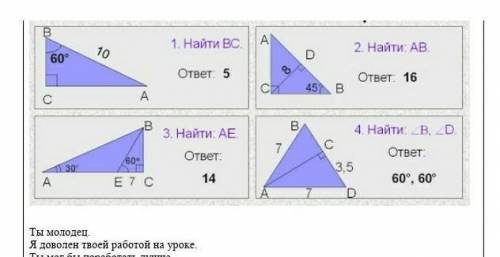
Задача 1.
Найдем ∠А = 90°-60° = 30°.
Катет ВС находится напротив угла 30°, а значит, что он равен половине гипотенузы ВА, то есть 10:2=5.
ответ: ВС= 5.
Задача 2.
Найдем ∠А = 90°-45° = 45°.
Значит, ΔАСВ - равнобедренный, АС=СВ.
Высота равнобедренного треугольника, проведенная к основанию, является и биссектрисой угла.
∠САВ = ∠ДСВ = 90:2 = 45°.
Тогда ΔСДВ - равнобедренный.
СД= ДВ как боковые стороны.
АВ = АД+ДВ = 8+8 = 16
ответ: 16.
Задача 3.
∠ЕВС = 90-60=30°
катет ЕС равен половине гипотенузы ЕВ, тогда ЕВ = 7+7=14
∠АЕВ = 180-60=120°
∠АВЕ = 180-120-30 = 30° (∠АВЕ).
Тогда ΔАВЕ - равнобедренный,
основания АЕ=ЕВ = 14
ответ: АЕ = 14
Задача 4.
Так как АВ=АД = 7 (по условию), то ΔАВД - равнобедренный.
∠В=∠Д.
В ΔАСД катет СД = 3,5, то есть половине гипотенузы АД (которая равна 7). Из этого следует, что напротив стороны СД находится угол 30° (∠САД).
Соответственно, что ∠СДА = 60° (90°-30°=60°).
У равнобедренного треугольника углы при основании равны, значит
∠В = ∠Д = 60°.