ответ: 5:3
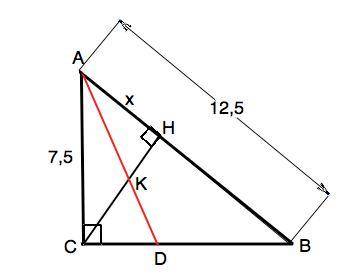
Объяснение: Биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Обозначим точку пересечения биссектрисы АD и высоты СН буквой К. Тогда СК:КН=АС:АН.
В прямоугольном треугольнике катет есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.
АС - катет, АН его проекция на гипотенузу. Примем АН=х ⇒ АС²=АВ•АН ⇒ 7,5²=12,5•х, откуда х=4,5
Искомое отношение СК:КН=7,5:4,5=5:3
диагональ основания = а√2, а - сторона основания
пусть диагональ основания - х
сторона основания а√2 = х, а = х√2/2
высота она же апофема равна х/2
тогда угол между несмежными боковыми гранями найдем из равнобедренного треугольника с боковыми сторона (апофемами) х/2
а основание есть сторона основания - х√2/2
отметим угол между плоскостями т.е между апофемами как "α"
опустим высоту в этом треугольника, которая будет делить этот треугольника на 2 равных прямоугольных ..из одного из них найдем sin α/2
sin α/2 = x√2/4 : х/2
sin α/2 = √2/2 т.е 45 градусов
тогда угол α = 90 градусов