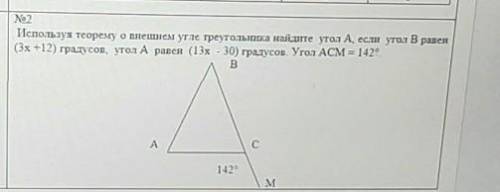
По теореме внешний угол треугольника равен сумме двух углов треугольника не смежных с ним.
угол АСМ и угол АСВ смежные и в сумме дают 180°. => АСВ=180°-142°=38°
=> составим уравнение и решим его
(3х+12)°+(13х-30)°=142°
3х+12+13х-30=142°
16х-18=142°
16х=142°+18°
16х=160°
х=10°
Угол А =13х-30=13*10-30=130-30=100°
угол В= 3х+12=3*10+12= 30+12=42°
Обозначим равные катеты прямоугольного треугольника - а.
АК и ВМ - медианы. Медианы, проведенные к равным сторонам, равны. АК = ВМ.
Из прямоугольного треугольника САК по теореме Пифагора найдем медиану АК:
АК = √(АС² + СК²) = √(а² + (a/2)²) = √(a² + a²/4) = √(5a²/4) = a√5/2
Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины, тогда
OK = ОМ = 1/3 AK = a√5/6
AO = ВО = 2·OK = a√5/3
Из треугольника ОКВ по теореме косинусов:
KB² = KO² + OB² - 2·KO·OB·cosα
a²/4 = (a√5/6)² + (a√5/3)² - 2 · a√5/6 · a√5/3 · cosα
a²/4 = 5a²/36 + 5a²/9 - 2 · 5a²/18 · cosα
1/4 = 5/36 + 5/9 - 5/9 · cosα
cosα = (25/36 - 1/4) : (5/9) = 16/36 · 9/5 = 4/9 · 9/5 = 4/5 = 0,8
По таблице Брадиса находим, что
α ≈ 37°
<А=100°
Объяснение:
<АСМ=<А+<В, теорема о внешнем угле.
13х-30+3х+12=142
16х=142+18
х=160/16
х=10
<А=(13х-30)=13*10-30=130-30=100°