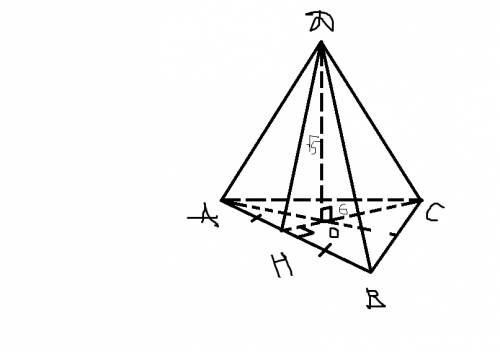
Рассмотрим треугольниу ABC-равносторонний(т.к.DABCD-прав. пирамида) OH=CH/3=6/3=2 (см)(в точке пересечения медианы делятся в отношении 2:1 от вершины)
Рассм. треуг. ODH-прямоуг. По теореме Пифагора DH=корень из DO^2+OH^2=корень из 5+4=корень из 9=3 (см)
Sпп=Sбп+Sосн
Рассм. треуг BCH-прямоуг.
sinB=MC/BC
sin60=6/BC
BC=6/(корень из 3/2)(под корнем только 3)=12/корень из 3=12 корней из 3/3=4 корня из 3(см)
Pосн=3*4 корня из 3=12 корней из 3 (см)
Sбп=1/2*DH*Pосн
Sбп=1/2*3*12 корней из 3=18корней из 3(см^2)
Sосн=1/2*CH*AB=1/2*6*4 корня из 3=12корней из3 (см^2)
Sпп=18корней из 3+12 корней из 3= 30 корней из3 (см^2)
1.обзначим трапецию ABCD, где AD - большее основание.
2. теперь определяем, что высотой в данной трапеции является не только перпендикулярная сторона, но и диаметр вписанной окружности (О - ее центр, К - точка касания с AD, М - точка касания с CD), найдем его.
3. по свойству касательной к окружности отрезки касательных равны, т.е. KD=MD=4=r, а т.к. d(диаметр)=2r, то d(она же высота)=4*2=8.
ответ: 8