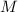на плоскость ромба -- точка 
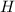. Пусть основания перпендикуляров из 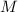на стороны ромба -- 
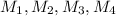(не важно, в каком порядке). Тогда, по теореме о трёх перпендикулярах, отрезки 
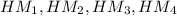перпендикулярны отрезку 
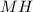. Таким образом, мы получаем четыре прямоугольных треугольника: 
, у которых общий катет 
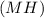и равны гипотенузы (по условию 
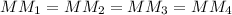), значит, все эти прямоугольные треугольники равны друг другу. Значит, 
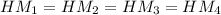, таким образом, точка 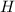так же равноудалена от сторон ромба, то есть лежит в центре вписанной окружности ромба, то есть на пересечении биссектрис, то есть это точка пересечения диагоналей (т. к. в ромбе диагонали являются биссектрисами).Пусть вершины ромба -- 
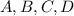(так, что диагональ 
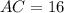, а диагональ 
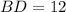). Тогда расстояние 
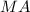является гипотенузой прямоугольного треугольника 
, катет 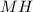которого нам дан в условии, а катет 
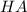находим исходя из того, что точка 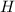-- точка пересечения диагоналей в ромбе, поэтому делит их пополам. Значит,
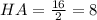. По теореме пифагора находим . 
. 
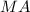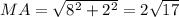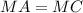, т. к. прямоугольные треугольники и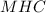 
равны по двум катетам.
. 
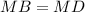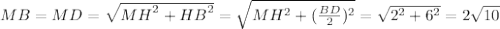
0,5*(6+8)*5=35