 °
° ° + 13° =
° + 13° = 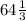 °
° °;
°;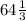 °
°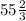 °
°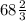 °
° °
° °
° 
Объяснение:
1)Дано :на рисунке ∠ADB=∠CBD=90° , ∠ADB=∠CBD.
Доказать :AD║BC
Доказательство.
ΔАВD=ΔСDВ ,как прямоугольные(∠ADB=∠CBD=90°) по равным гипотенузам BD-общая,и равным острым углам ∠ADB=∠CBD по условию. В равных треугольниках соответственные элементы равны ⇒∠ADB=∠CBD. . И эти углы накрест лежащие при DB-секущей⇒AD║BC . по признаку накрест лежащих углов.
2)Дано: на чертеже ∠А=70°,∠АОD=90°,∠С=20°.
Доказать: AD║BC .
Доказательтво.
ΔAOD-прямоугольный. По т. о сумме углов треугольника ∠ODA=180°-90°-70°=20°.
Углы ∠AOD= ∠BOC=20° и по расположению они накрест лежащие⇒AD║BC при CD-секущей по признаку накрест лежащих углов.
3) Дано :ΔАВС-прямоугольный, ∠С=60°,∠ВВ₁⊥АС, ВВ₁=2 см.
Найти :АВ.
Решение.
ΔАВС-прямоугольный, ∠С=60°, значит ∠ВАС=90°-60°=30° по свойству острых углов прямоугольного треугольника..
ΔАВВ₁ -прямоугольный , ∠ВАС=30° .По свойству угла в 30° имеем ВВ₁=1/2*АВ или 2=1/2*АВ или АВ=4 см
Берём осевое сечение плоскостью шара-цилиндра.
Получаем диаметр шара D = sqrt(20^2+(2*5)^2)) = 10*sqrt(5)
Объём шара V = 4/3 *pi*R^3 = 4/3 *pi* (5*sqrt(5))^3
Объём цилиндра W = H*S = H*pi*r^2 = 20*pi*5^2
V/W =500/3 *pi*sqrt(5)/100*pi = 5*sqrt(5)/3