1. Противоположные стороны параллелограмма попарно равны.
2. Противоположные углы параллелограмма попарно равны.
3. Сумма градусных мер двух смежных углов параллелограмма равна 180°.
4. Сумма всех углов параллелограмма равна 360°.
5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
6. Точка пересечения диагоналей является центром симметрии параллелограмма.
7. Диагонали d₁ и d₂ и стороны a и b параллелограмма связаны следующим соотношением: 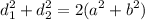
8. Биссектриса отсекает от параллелограмма равнобедренный треугольник.
Решение.
1. Найти косинус наименьшего угла треугольника. Это угол С.
Напротив наименьшей стороны лежит наименьший угол. Значит, напротив угла С лежит сторона АВ=4.
Теорема косинусов гласит: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
Для треугольника АВС:
АВ²= ВС²+АС²–2×ВС×АС×cos∠C;
4²= 5²+7²–2×5×7×cos∠C;
16= 25+49–70cos∠C;
70cos∠C= 25+49–16;
70cos∠C= 58;
cos∠C= 58/70, это приблизительно, если округлить до тысячных равно 0,829.
Записываем в ответ:
cos∠C= 0,829.
2. Если воспользоваться калькулятором и посчитать значение угла С, а потом округлить его до целых, то выйдет ∠С=34°.
Объяснение:
1. Противоположные стороны параллелограмма попарно равны
2. Противоположные углы параллелограмма попарно равны
3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов
4. Сумма всех углов равна 360°
5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
6. Точка пересечения диагоналей является центром симметрии параллелограмма
7. Биссектриса отсекает от параллелограмма равнобедренный треугольник