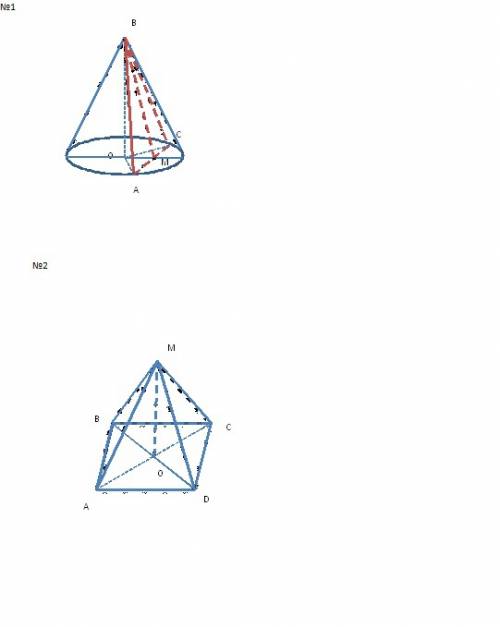
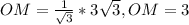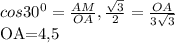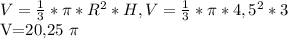Один из катетов прямоугольного треугольника равен 8 см, а второй меньше гипотенузы на 4 см. Найдите гипотенузу. 14

6

10

5

Вопрос №2 ?

В прямоугольный треугольник вписана окружность. Точка касания делит один из катетов на отрезки длиной 3 см и 5 см, считая от вершины прямого угла. Найдите гипотенузу.

17

12

15

13

Вопрос №3 ?

У параллелограмма ABCD сторона AB равна 17, а сторона AD делится высотой BE на отрезки AE=8, ED=20. Найдите диагональ BD параллелограмма.

28

25

20

15

Вопрос №4 ?

Стороны треугольника равны 9, 11 и 12. Найдите проекцию наименьшей стороны на наибольшую.

17/3

13/3

5

23/3

Вопрос №5 ?

Диагональ равнобедренной трапеции перпендикулярна боковой стороне. Основания трапеции равны 10 и 26. Найдите высоту трапеции.

12

6

144

24

Вопрос №6 ?

Две башни, одна из которых 40 футов, а вторая – 30 футов в высоту, расположены на расстоянии 50 футов одна от другой. К колодцу, который находится между ними, одновременно с двух башен взлетело по птице. Двигаясь с одинаковой скоростью, они прилетели к колодцу одновременно. Найдите расстояние от колодца до ближайшей башни (в футах).

Вопрос №7 ?

Точка касания окружности, вписанной в равнобокую трапецию, делит ее боковую сторону на отрезки длиной 8 см и 2 см. Найдите радиус вписанной окружности (в см).

👇

Увидеть ответ

Ответ:

irinaa10

29.01.2021

каланча ВАК км на ага каке

4,8(18 оценок)

Открыть все ответы

Ответ:

simpleam

29.01.2021

Сечение конуса - ΔАВС с основанием АС=6√3 - хорда.
равнобедренный ΔАОС (О - центр основания конуса): АО=ОС=R, <AOC=120°, <OAC=<OCA=30°, OM_|_AC, ОМ - высота, медиана ΔАОС, ⇒АМ=3√3.
tg30°=OM:AM.

$OM= \frac{1}{ \sqrt{3} } *3 \sqrt{3} , OM=3$

$cos30^{0} = \frac{AM}{OA}, \frac{ \sqrt{3} }{2} = \frac{OA}{3 \sqrt{3} } 

OA=4,5

$

по условию, секущая плоскость составляет с плоскостью основания угол 45°, ⇒ линейный угол ВАСМ - угол ВМО=45°. высота конуса Н=ОМ=3

$V= \frac{1}{3}* \pi * R^{2}*H, V= \frac{1}{3} * \pi * 4,5^{2} *3

V=20,25 \pi 
 
$
ответ: Vк=20,25π

2. MABCD - правильная пирамида с диагональю основания АС=d, угол между боковым ребром МА и плоскостью основания <MAC= α
MO_|_(MABCD), МО - высота пирамиды.
прямоугольный ΔМОА: ОА=d/2, <A=α. tgα=MO:OA, MO=tgα*OA
MO=d*tgα/2

Vпир=(1/3)*Sосн*H
Sосн=a², a- сторона основания пирамиды
диагональ пирамиды найдена по теореме Пифагора из ΔАВС: АС²=АВ²+АС²
АВ=АС=а
d²=a²+a², d²=2a². d=a√2, ⇒a=d/√2
S=(d/√2)²=d²/2
Vпир=(1/3)*(d²/2)*(d*tgα/2)
Vпир=(d³ *tgα)/12

Решить (с рисунком) 1)через вершину конуса проведена плоскость пересекающая окружность основания по

Решить (с рисунком) 1)через вершину конуса проведена плоскость пересекающая окружность основания по

4,8(29 оценок)

Ответ:

Zen201

29.01.2021

Значит так. Чертим прямоугольный треугольник.
Решение: Рассмотрим треугольник ACH: Так как CH - высота,то этот треугольник прямоугольный. Следовательно CH - катет и мы находим его по теореме Пифагора: CH = √6^²-4^² = √36-16 = √20 = 2√5
Я предлагаю рассмотреть треугольник ABC и найти x через CB(не знаю можно ли так,как я решил,но я запишу)
AB=4+x
CB=√AB²-AC² = √(4-x)²-6² = √x²-10x-20
Разбираем квадратичное уравнение:
x²-10x-20=0
D= 100+4*20=180 √D= 6√5
x_{12} = 5+-3√5
x2 - не подходит,так как получается отрицательным,поэтому BH = 5+3√5.
ответ: 5+3√5
Впрямоугольном треугольнике abc с прямым углом c проведена высота ch. чему равен отрезок bh, если ac