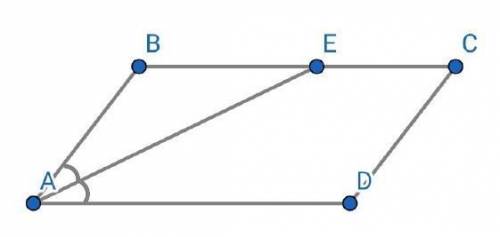
Четырёхугольник ABCD — параллелограмм.
Отрезок АЕ — биссектриса ∠А.
Е ∈ ВС.
ВЕ = 3*ЕС.
ВС = 12 [см].
Найти :Р(ABCD) = ?
Решение :Пусть ЕС = х, тогда, по условию задачи, ВЕ = 3х.
ВС = ВЕ + ЕС
12 [см] = 3х + х
4х = 12 [см]
х = 3 [см].
ВЕ = 3х = 3*3 [см] = 9 [см].
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.Следовательно, ∆АВЕ — равнобедренный (причём ВЕ = АВ = 9 [см]).
Периметр параллелограмма равен удвоенной сумме его смежных сторон.Следовательно, Р(ABCD) = 2*(AB + BC) = 2*(9 [см] + 12 [см) = 2*21 [см] = 42 [см].
ответ :42 [см].
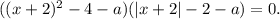 . Произведение равно нулю, если хотя бы один из множителей равен нулю, т.е.
. Произведение равно нулю, если хотя бы один из множителей равен нулю, т.е. 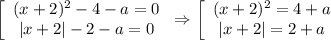 .
.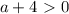 и
и 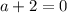 или
или 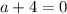 и
и 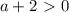
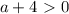 откуда
откуда 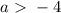 и
и 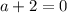 откуда
откуда 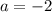 .
.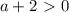 откуда
откуда 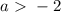 и
и 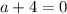 откуда
откуда  .
.
Пусть ABC и A1B1C1 основания О и O1 центры оснований Центр X сферы лежит на средине OO1, XO=a/2, AO=2/3*(Кор(3)/2)a, (2/3 медианы основания),XA=R (Искомый радиус).
XO^2+AO^2=XA^2=R^2=(a^2)/4+(a^2)/3=7/12*a^2
R=кор(7/12)*a