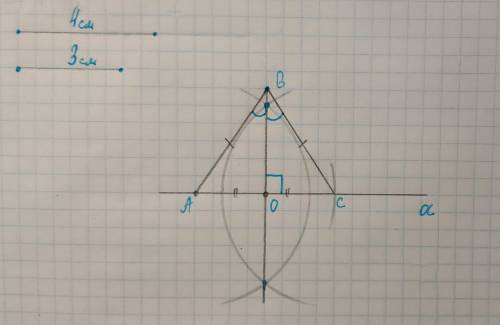
1. Построила на рисунке. Масштаб фотографии разный у всех, я взяла длину основания 4см и длину биссектрисы 3см. Свойством пользовалась тем, что в равнобедренном треугольнике биссектриса, проведённая к основанию, является его медианой. Построила медиану по алгоритму построения середины отрезка.
2. Треугольник равнобедренный, т.к. ВО⊥АС, угол АВО=СВО, АО=ОС. Можно измерить сторону и биссектрису. Всё соблюдается.
3. Задача будет иметь решение в том случае, если при построении сумма двух любых сторон треугольника будет больше длины третьей стороны. Т.е. основание не должно быть дано длиннее, чем сумма боковых сторон.
Даны точка M (3,-2,1) и векторы l(1,-2,4) и m(-3,0,4)
Для начала находим координаты вектора, перпендикулярного искомой плоскости. Таковым является векторное произведение заданных векторов:
i j k | i j
1 -2 4 | 1 -2
-3 0 4 | -3 0 = -8i - 12j + 0i - 4j -0i - 6k = -8i - 16j - 6k.
Координаты (-8; -16; -6). Вспомним, что в уравнении плоскости Ax+By+Cz+D=0 вектор (A;B;C) является вектором, перпендикулярной заданной плоскости. Поэтому искомое уравнение имеет вид -8x - 16y - 6z + D = 0 .
Остается найти свободный коэффициент D - его найдем из условия, что плоскость проходит через точку M(3; -2; 1). Подставляем значения в уравнение:
-8*3-16*(-2)-6*1+D = 0
D = 24-32+6 = -2
Искомое уравнение -8x-16y-6z-2=0.
Можно сократить на -2: 4x+8y+3z+1=0.
Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Пусть а, в, с - длина ребер параллелепипеда
d - диагональ параллелепипеда
d=√a²+b²+c²
Диагональ делит каждую грань(прямоугольник) параллелепипеда на 2 равных прямоугольных треугольника, в которых диагональ грани - гипотенуза, а ребра-катеты.
Составим систему уравнений, используя теорему Пифагора:
√a²+b²=2√17
√c²+b²=10
√a²+c²=2√10
Возведем обе части уравнений в квадрат:
а²+b²=68
+ c²+b²=100
a²+c²=40
2a²+2b²+2c²=208
a²+b²+c²=104
d²=104
d=√104≈10,2