Question

Найдите площадь ромба с углом в 30 градусов, если площадь круга, вписанного в него равна 10пи.

Answer 1

Есть в данном случае две формулы для вычисления площади ромба

 Первая формула.

$S=p*r$, где r - радиус вписанной окружности. p - полупериметр ромба.

В данном случае полупериметр ромба равен 2а, где а - сторона ромба.

Формула принимает вид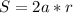 $S=2a*r$

Найдем радиус круга. Площадь круга равна

$S_{circ}=\pi*r^2$

$10\pi=\pi*r^2$

$r^2=10$

$r=\sqrt{10}$

Значит формула приобретает вид

$S=2a*\sqrt{10}$

Другая (вторая) формула исходит из формулы параллелограмма

$S=a^2*\sin 30^\circ$

Приравняем правые части формулы

$2a*\sqrt{10}=a^2\sin30^\circ$

$2a*\sqrt{10}=a^2*0,5$

Умножим обе части на 2

$4a*\sqrt{10}=a^2$

Сократим обе части на а.

$4\sqrt{10}=a$

Или $a=4\sqrt{10}$

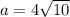
Подставим в формулу

$S=a^2*\sin 30^\circ$

$S=(4*\sqrt{10})^2*\sin 30^\circ$

$S=(4*\sqrt{10})^2*0,5$

$S=160*0,5$

S=80 - площадь ромба

ответ: 80 - квадратных единиц площадь ромба.

Answer 2

пл р=сторона на высоту =а*h

пл кр=10пи=пи r^2 из пл круга выразим его радиус 

радиус=корень из 10

диаметр=2*радиуса=2*корень из 10

сторона против 30 гр = половине гипотенезы значит сторона ромба равна 4* корень из 10

отсюда найдем пл ромба 

s=4* корень из 10*2 * корень из 10=80

ответ 80